
如图,△ABC的边BC在直线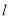 上,AC⊥BC,且AC=BC,△EFP的边FP也在直线
上,AC⊥BC,且AC=BC,△EFP的边FP也在直线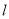 上,边EF与边AC重合,且EF=FP。
上,边EF与边AC重合,且EF=FP。
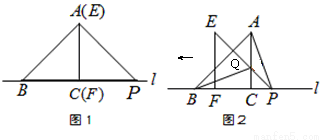
(1)在图1中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线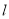 向左平移到图2的位置时,EP交AC于点Q,连结AP、BQ。猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想。
向左平移到图2的位置时,EP交AC于点Q,连结AP、BQ。猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想。
(1)∠PEF=45°,∠BAP=45°+45°=90°,AB=AP且AB⊥AP.(2)AP⊥B
【解析】
试题分析:(1)根据等腰直角三角形性质得出AB=AP,∠BAC=∠PAC=45°,求出∠BAP=90°即可;
(2)求出CQ=CP,根据SAS证△BCQ≌△ACP,推出AP=BQ,∠CBQ=∠PAC,根据三角形内角和定理求出∠CBQ+∠BQC=90°,推出∠PAC+∠AQG=90°,求出∠AGQ=90°即可.
试题解析:(1)AB=AP且AB⊥AP,
证明:∵AC⊥BC且AC=BC,
∴△ABC为等腰直角三角形,
∴∠BAC=∠ABC= (180°-∠ACB)=45°,
(180°-∠ACB)=45°,
又∵△ABC与△EFP全等,
同理可证∠PEF=45°,
∴∠BAP=45°+45°=90°,
∴AB=AP且AB⊥AP.
(2)BQ与AP所满足的数量关系是AP=BQ,位置关系是AP⊥BQ,
证明:延长BQ交AP于G,
由(1)知,∠EPF=45°,∠ACP=90°,
∴∠PQC=45°=∠QPC,
∴CQ=CP,
∵∠ACB=∠ACP=90°,AC=BC,
∴在△BCQ和△ACP中
BC=AC
∠BCQ=∠ACP
CQ=CP,
∴△BCQ≌△ACP(SAS),
∴AP=BQ,∠CBQ=∠PAC,
∵∠ACB=90°,
∴∠CBQ+∠BQC=90°,
∵∠CQB=∠AQG,
∴∠AQG+∠PAC=90°,
∴∠AGQ=180°-90°=90°,
∴AP⊥BQ.
考点:全等三角形的判定与性质;等腰直角三角形


科目:初中数学 来源:2016届河北省邢台市沙河市七年级下学期期末数学试卷(解析版) 题型:解答题
(1)计算:9x2+x-(3x+2)(3x-2);
(2)因式分【解析】
(x+y)2-4xy;
(3)解不等式组 ,并把解集在数轴表示出来.
,并把解集在数轴表示出来.
查看答案和解析>>
科目:初中数学 来源:2016届河北省滦南县七年级下学期期中考试数学试卷(解析版) 题型:选择题
如图,面积为12cm2的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积为( )
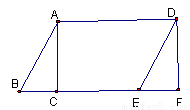
A.24cm2 B.36cm2 C.48cm2 D.无法确定
查看答案和解析>>
科目:初中数学 来源:2016届江西省抚州市黎川县七年级下学期期末数学试卷(解析版) 题型:选择题
口袋中装有若干个红球,6个白球,从袋中任意摸一个球,摸到白球的概率是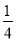 ,那么口袋中红球有( )
,那么口袋中红球有( )
A.18个 B.12个 C.6个 D.2个
查看答案和解析>>
科目:初中数学 来源:2016届江西省吉安市六校七年级下学期联考数学试卷(解析版) 题型:解答题
小明和妹妹做游戏:在一个不透明的箱子里放入20张纸条(除所标字母外其余相同),其中12张纸条上字母为A,8张纸条上的字母为B,将纸条摇匀后任意摸出一张,如果摸到纸条上的字母为A,则小明胜;如果摸到纸条上的字母为B,则妹妹胜。
(1)这个游戏公平吗?请说明理由;
(2)若妹妹在箱子中再放入3张与前面相同的纸条,所标字母为B,此时这个游戏对谁有利?
查看答案和解析>>
科目:初中数学 来源:2016届江苏省苏州市七年级下学期期末考试数学试卷(解析版) 题型:选择题
下列条件中,不能判定△ABC≌△A'B'C'的是( )
A.∠A=∠A',∠C=∠C',AC=A'C'
B.∠C=∠C'=90°,BC=B'C',AB=A'B'
C.∠A=∠A'=80°,∠B=60°,∠C'=40°,AB=A'B'
D.∠A=∠A',BC=B'C',AB=A 'B'
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com