
【题目】在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,3),抛物线顶点为D点.
(1)求此抛物线解析式;
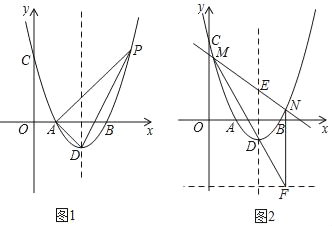
(2)如图1,点P为抛物线上的一个动点,且在对称轴右侧,若△ADP面积为3,求点P的坐标;
(3)在(2)的条件下,PA交对称轴于点E,如图2,过E点的任一条直线与抛物线交于M,N两点,直线MD交直线y=﹣3于点F,连结NF,求证:NF∥y轴.
【答案】(1)抛物线解析式为:y=x2﹣4x+3;(2)P(4,3);(3)证明见解析.
【解析】
(1)利用待定系数法确定函数关系式;
(2)利用待定系数法求得直线AD的解析式,根据函数图象上点的坐标特征可以设P(t,t2-4t+3),R(t,-t+1).如图1,过点P作PR∥y交AD的延长线于R,由此得到S△ADP=S△APR-S△PDR=![]() PR(t-1)-
PR(t-1)-![]() PR(t-2)=3,PR=6,所以利用关于t的方程求得点P的坐标;
PR(t-2)=3,PR=6,所以利用关于t的方程求得点P的坐标;
(3)欲证明NF∥y轴,只需求得点N、F的横坐标相等即可.
(1)把A(1,0),B(3,0),C(0,3)分别代入y=ax2+bx+c,得
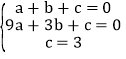 ,
,
解得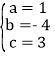 ,
,
所以,该抛物线解析式为:y=x2﹣4x+3;
(2)由(1)知,该抛物线解析式为:y=x2﹣4x+3,
∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴顶点D的坐标是(2,﹣1).
如图1,过点P作PR∥y交AD的延长线于R,
由A(1,0),D(2,﹣1)易得直线AD的解析式为:y=﹣x+1.
设P(t,t2﹣4t+3),R(t,﹣t+1).
∴PR=t2﹣3t+2.
∵△ADP面积为3,
∴S△ADP=S△APR﹣S△PDR=![]() PR(t﹣1)﹣
PR(t﹣1)﹣![]() PR(t﹣2)=3,
PR(t﹣2)=3,
∴PR=6,即t2﹣3t+2=6,
解得t1=4,t2=0(舍去).
此时t2﹣4t+3=42﹣4×4+3=3,
∴P(4,3);
(3)证明:∵P(4,3),A(1,0),
∴直线AP为y=x﹣1,
把x=2代入,y=1,
故E(2,1).
设直线MN的解析式为:y=kx﹣2k+1.
联立方程组,得![]() ,
,
消去y,得x2﹣(4+k)x+2+2k=0,
解得x1=![]() ,x2=
,x2=![]() ,
,
∴M(![]() ,
,![]() ),xN=
),xN=![]() .
.
∴直线MN的解析式为y=![]() (x﹣2)﹣1.
(x﹣2)﹣1.
令y=﹣3,得xF=![]() ,
,
即:xN=xF,
∴NF∥y轴.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】为了更好地保护美丽如画的邛海湿地,西昌市污水处理厂决定先购买A,B两种型号的污水处理设备共20台,对邛海湿地周边污水进行处理.每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640 t,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1 080 t.
(1)求A,B两种型号的污水处理设备每周每台分别可以处理污水多少吨.
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4 500 t,请你列举出所有购买方案,并指出哪种方案所需资金最少,最少是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有标号分别为1,2,3,4的四个球,这些球除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的球的概率;
(2)甲、乙两人用这四个小球玩摸球游戏,规则是:甲从盒中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,乙再从盒中随机摸出一个小球,并记下标号数字.若两次摸到球的标号数字同为奇数或同为偶数,则判甲赢;若两次摸到球的标号数字为一奇一偶,则判乙赢.请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平行四边形![]() 在平面直角坐标系中,其中点
在平面直角坐标系中,其中点![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,点
,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,
(1)点![]() 的坐标为______,点
的坐标为______,点![]() 的坐标为_______.
的坐标为_______.
(2)求点![]() 的坐标.
的坐标.
(3)如图2,根据(2)中结论,将![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,求
,求![]() 的长度.
的长度.
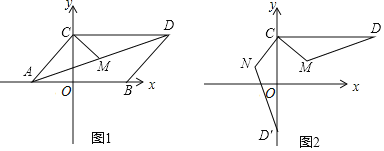
查看答案和解析>>
科目:初中数学 来源: 题型:
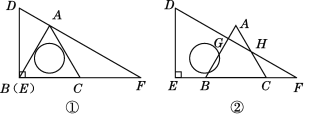
【题目】已知△ABC是等边三角形,将一块含有30°角的直角三角尺DEF按如图所示放置,让三角尺在BC所在的直线上向右平移.如图①,当点E与点B重合时,点A恰好落在三角尺的斜边DF上.
(1)利用图①证明:EF=2BC.
(2)在三角尺的平移过程中,在图②中线段AH=BE是否始终成立(假定AB,AC与三角尺的斜边的交点分别为G,H)?如果成立,请证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点的坐标分别为A (0,2),B(﹣1,0),点C为线段AB的中点,现将线段BA绕点B按逆时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)、经过点D.
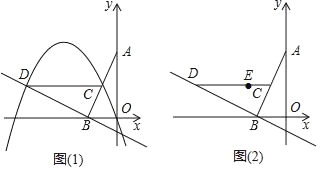
(1)如图1,若该抛物线经过原点O,且a=﹣1.
①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由.
(2)如图2,若该抛物线y=ax2+bx+c(a<0)经过点E(﹣1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余,若符合条件的Q点的个数是4个,请直接写出a的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进甲、乙两种商品共![]() 件,这两种商品的进价、售价如表所示:
件,这两种商品的进价、售价如表所示:
进价(元/件) | 售价(元/件) | |
甲种商品 |
|
|
乙种商品 |
|
|
设购进甲种商品![]() (
(![]() ,且
,且![]() 为整数)件,售完此两种商品总利润为
为整数)件,售完此两种商品总利润为![]() 元.
元.
(1)该商场计划最多投入![]() 元用于购进这两种商品共
元用于购进这两种商品共![]() 件,求至少购进甲种商品多少件?
件,求至少购进甲种商品多少件?
(2)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)若售完这些商品,商场可获得的最大利润是__________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣![]() x2+4x-
x2+4x-![]() .
.
(1)用配方法把该函数解析式化为y=a(x﹣h)2+k的形式,并指出函数图象的对称轴和顶点坐标;
(2)求函数图象与x轴的交点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com