
【题目】已知二次函数y=﹣![]() x2+4x-
x2+4x-![]() .
.
(1)用配方法把该函数解析式化为y=a(x﹣h)2+k的形式,并指出函数图象的对称轴和顶点坐标;
(2)求函数图象与x轴的交点坐标.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
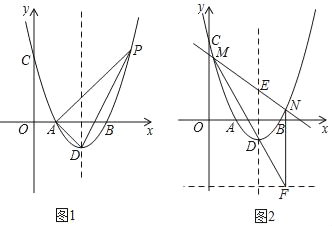
【题目】在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,3),抛物线顶点为D点.
(1)求此抛物线解析式;
(2)如图1,点P为抛物线上的一个动点,且在对称轴右侧,若△ADP面积为3,求点P的坐标;
(3)在(2)的条件下,PA交对称轴于点E,如图2,过E点的任一条直线与抛物线交于M,N两点,直线MD交直线y=﹣3于点F,连结NF,求证:NF∥y轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位举行“健康人生”徒步走活动,某人从起点体育村沿建设路到市生态园,再沿原路返回,设此人离开起点的路程s(千米)与徒步时间t(小时)之间的函数关系如图所示,其中从起点到市生态园的平均速度是4千米/小时,用2小时,根据图象提供信息,解答下列问题.
(1)求图中的a值.
(2)若在距离起点5千米处有一个地点C,此人从第一次经过点C到第二次经过点C,所用时间为1.75小时.
①求AB所在直线的函数解析式;
②请你直接回答,此人走完全程所用的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
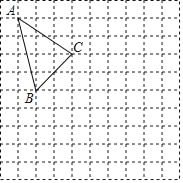
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点△ABC(顶点在网格线的交点上)的顶点A、C的坐标分别为A(﹣3,4)C(0,2)
(1)请在网格所在的平面内建立平面直角坐标系,并写出点B的坐标;
(2)画出△ABC关于原点对称的图形△A1B1C1;
(3)求△ABC的面积;
(4)在x轴上存在一点P,使PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆假期期间,某单位8名领导和320名员工集体外出进行素质拓展活动,准备租用45座大车或30座小车.若租用2辆大车3辆小车共需租车费1700元;若租用3辆大车2辆小车共需租车费1800元
(1)求大、小车每辆的租车费各是多少元?
(2)若每辆车上至少要有一名领导,每个人均有座位,且总租车费用不超过3100元,求最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点.
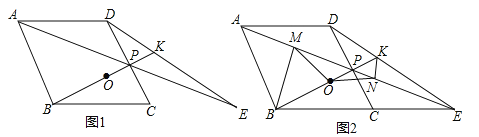
(1)求证:△ADP≌△ECP;
(2)若BP=nPK,试求出n的值;
(3)作BM丄AE于点M,作KN丄AE于点N,连结MO、NO,如图2所示,请证明△MON是等腰三角形,并直接写出∠MON的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com