
【题目】如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点.
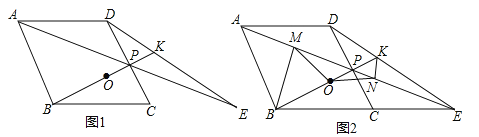
(1)求证:△ADP≌△ECP;
(2)若BP=nPK,试求出n的值;
(3)作BM丄AE于点M,作KN丄AE于点N,连结MO、NO,如图2所示,请证明△MON是等腰三角形,并直接写出∠MON的度数.
【答案】(1)证明见试题解析;(2)3;(3)证明见试题解析,120°.
【解析】
试题(1)由菱形的性质得到AD∥BC,根据由平行线的性质得到∠DAP=∠CEP,∠ADP=∠ECP,根据全等三角形的判定定理证明结论;
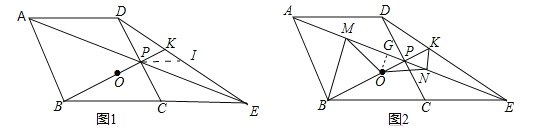
(2)作PI∥CE交DE于I,由点P是CD的中点证明CE=2PI,BE=4PI,根据相似三角形的性质证明结论;
(3)作OG⊥AE于G,由平行线等分线段定理得到MG=NG,又OG⊥MN,可证明△MON是等腰三角形,由直角三角形的性质和锐角三角函数求出∠MON的度数.
试题解析:(1)∵四边形ABCD为菱形,∴AD∥BC,∴∠DAP=∠CEP,∠ADP=∠ECP,在△ADP和△ECP中,∵∠DAP=∠CEP,∠ADP=∠ECP,DP=CP,∴△ADP≌△ECP;
(2)如图1,作PI∥CE交DE于I,则![]() ,又点P是CD的中点,∴
,又点P是CD的中点,∴![]() ,∵△ADP≌△ECP,∴AD=CE,∴
,∵△ADP≌△ECP,∴AD=CE,∴![]() ,∴BP=3PK,∴n=3;
,∴BP=3PK,∴n=3;
(3)如图2,作OG⊥AE于G,∵BM丄AE于,KN丄AE,∴BM∥OG∥KN,∵点O是线段BK的中点,∴MG=NG,又OG⊥MN,∴OM=ON,即△MON是等腰三角形,由题意得,△BPC,△AMB,△ABP为直角三角形,设BC=2,则CP=1,由勾股定理得,BP=![]() ,则AP=
,则AP=![]() ,根据三角形面积公式,BM=
,根据三角形面积公式,BM=![]() ,由(2)得,PB=3PO,∴OG=
,由(2)得,PB=3PO,∴OG=![]() BM=
BM=![]() ,MG=
,MG=![]() MP=
MP=![]() ,tan∠MOG=
,tan∠MOG=![]() ,∴∠MOG=60°,∴∠MON的度数为120°.
,∴∠MOG=60°,∴∠MON的度数为120°.


科目:初中数学 来源: 题型:
【题目】某商场计划购进甲、乙两种商品共![]() 件,这两种商品的进价、售价如表所示:
件,这两种商品的进价、售价如表所示:
进价(元/件) | 售价(元/件) | |
甲种商品 |
|
|
乙种商品 |
|
|
设购进甲种商品![]() (
(![]() ,且
,且![]() 为整数)件,售完此两种商品总利润为
为整数)件,售完此两种商品总利润为![]() 元.
元.
(1)该商场计划最多投入![]() 元用于购进这两种商品共
元用于购进这两种商品共![]() 件,求至少购进甲种商品多少件?
件,求至少购进甲种商品多少件?
(2)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)若售完这些商品,商场可获得的最大利润是__________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣![]() x2+4x-
x2+4x-![]() .
.
(1)用配方法把该函数解析式化为y=a(x﹣h)2+k的形式,并指出函数图象的对称轴和顶点坐标;
(2)求函数图象与x轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,请回答下列问题
材料一:我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积.用现代式子表示即为:S=![]() …①(其中a,b,c为三角形的三边长,S为面积)而另一个文明古国古希腊也有求三角形面积的“海伦公式”;S=
…①(其中a,b,c为三角形的三边长,S为面积)而另一个文明古国古希腊也有求三角形面积的“海伦公式”;S=![]() ……②(其中p=
……②(其中p=![]() )
)
材料二:对于平方差公式:a2﹣b2=(a+b)(a﹣b)
公式逆用可得:(a+b)(a﹣b)=a2﹣b2,
例:a2﹣(b+c)2=(a+b+c)(a﹣b﹣c)
(1)若已知三角形的三边长分别为3、4、5,请试分别运用公式①和公式②,计算该三角形的面积;
(2)你能否由公式①推导出公式②?请试试.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了三项素质测试.各项测试成绩如表格所示:
测试项目 | 测试成绩 | ||
甲 | 乙 | 丙 | |
专业知识 | 74 | 87 | 90 |
语言能力 | 58 | 74 | 70 |
综合素质 | 87 | 43 | 50 |
(1)根据实际需要,公司将专业知识、语言能力和综合素质三项测试得分按4:3:1的比例确定每个人的测试总成绩,此时谁将被录用?
(2)请重新设计专业知识、语言能力和综合素质三项测试得分的比例来确定每个人的测试总成绩,使得乙被录用,若重新设计的比例为x:y:1,且x+y+1=10,则x= ,y= .(写出x与y的一组整数值即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
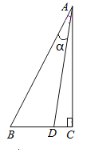
【题目】如图,已知Rt△ABC中,∠C=90°,∠BAC=30°,点D为边BC上的点,连接AD,∠BAD=α,点D关于AB的对称点为E,点E关于AC的对称点为G,线段EG交AB于点F,连接AE,DE,DG,AG.
(1)依题意补全图形;
(2)求∠AGE的度数(用含α的式子表示);
(3)猜想:线段EG与EF,AF之间是否存在一个数量关系?若存在,请写出这个数量关系并证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(![]() 表示时间,
表示时间,![]() 、
、![]() 表示路程),根据图象解答下列问题:
表示路程),根据图象解答下列问题:
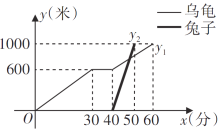
(1)“龟兔再次赛跑”的路程为__________米;
(2)它们两个约定__________先出发(填“兔子”和“乌龟”),先出发__________分钟;
(3)乌龟跑完全程用了__________分钟,兔子跑完全程用了__________分钟,乌龟平均速度是__________米/分,兔子平均速度是__________米/分;
(4)观察图象,你还能得出什么结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,点D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试写出线段BE,EF,FC之间的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com