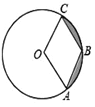
【题目】如图，已知⊙O的半径是4，点A,B,C在⊙O上，若四边形OABC为菱形，则图中阴影部分面积为（ ）
A. 
B. 
C. 
D. 
一诺书业暑假作业快乐假期云南美术出版社系列答案科目：初中数学 来源： 题型：
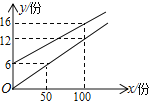
【题目】武汉市某校实行学案式教学，需印制若干份数学学案．印刷厂有甲、乙两种收费方式，除按印刷份数收取印刷费外，甲种方式还需收取制版费而乙种不需要，两种印刷方式的费用y（元）与印刷份数x（份）之间的关系如图所示
(1) 求甲、乙两种收费方式的函数关系式；
(2) 当印刷多少份学案时，两种印刷方式收费一样?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形
中，点
、
是正方形内两点，
，
，为探索这个图形的特殊性质，某数学兴趣小组经历了如下过程：
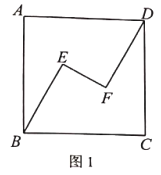
（1）在图1中，连接
，且
①求证：
与互相平分；
②求证：
；
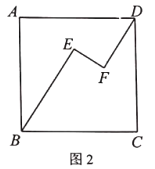
（2）在图2中，当
，其它条件不变时，是否成立？若成立，请证明：若不成立，请说明理由.
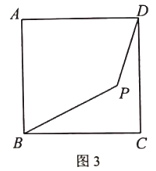
（3）在图3中，当
，
，
时，求
之长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，O为直线AB上一点，过点O作射线OC，∠AOC＝30°，将一直角三角板（∠M＝30°）的直角项点放在点O处，一边ON在射线OA上，另一边OM与OC都在直线AB的上方．
（1）将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周．如图2，经过t秒后，ON落在OC边上，则t＝ 秒（直接写结果）．
（2）在（1）的条件下，若三角板继续转动，同时射线OC也绕O点以每秒10°的速度沿逆时针方向旋转一周，当OC转动9秒时，求∠MOC的度数．
（3）在（2）的条件下，它们继续运动多少秒时，∠MOC＝35°？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“十一”黄金周期间，某风景区在7天假期中每天旅游的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）（单位：万人）,其中9月30日的游客人数为2万：
（1）请问10月2日的游客人数为多少？
（2）请判断7天内游客人数最多的是哪天？最少的是哪天？它们相差多少万人？
（3）求这一次黄金周期间该风景区游客总人数.（假设每天游客都不重复）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2﹣4ax+3a．
（Ⅰ）求该二次函数的对称轴；
（Ⅱ）若该二次函数的图象开口向下，当1≤x≤4时，y的最大值是2，且当1≤x≤4时，函数图象的最高点为点P，最低点为点Q，求△OPQ的面积；
（Ⅲ）若对于该抛物线上的两点P（x1，y1），Q（x2，y2），当t≤x1≤t+1，x2≥5时，均满足y1≥y2，请结合图象，直接写出t的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是小东设计的“作平行四边形ABCD，使∠B=45°，AB=2cm,BC=3cm”的作图过程．
（1）作法：如图，①画∠B=45°；
②在∠B的两边上分别截取BA=2cm,BC=3cm.
③以点A为圆心，BC长为半径画弧，以点
为圆心，AB长为半径画弧，两弧相交于点D；则四边形ABCD为所求的平行四边形．
根据小东设计的作图过程，
（1）使用直尺和圆规，补全图形；（保留作图痕迹）
（2）完成下面的证明．
证明：∵
_______，
_______，
∴四边形ABCD为所求的平行四边形．（____________）（填推理的依据）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】服装店10月份以每套500元的进价购进一批羽绒服，当月以标价销售，销售额14000元，进入11月份搞促销活动，每件降价50元，这样销售额比10月份增加了5500元，售出的件数是10月份的1.5倍．
（1）求每件羽绒服的标价是多少元；
（2）进入12月份，该服装店决定把剩余的羽绒服按10月份标价的八折销售，结果全部卖掉，而且这批羽绒服总获利不少于12700元，问这批羽绒服至少购进多少件？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
