
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 是正方形内两点,
是正方形内两点,![]() ,
,![]() ,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程:
,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程:
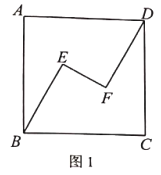
(1)在图1中,连接![]() ,且
,且![]()
①求证:![]() 与
与![]() 互相平分;
互相平分;
②求证:![]() ;
;
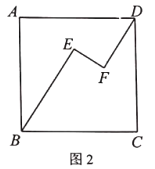
(2)在图2中,当![]() ,其它条件不变时,
,其它条件不变时,![]() 是否成立?若成立,请证明:若不成立,请说明理由.
是否成立?若成立,请证明:若不成立,请说明理由.
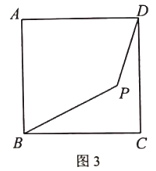
(3)在图3中,当![]() ,
,![]() ,
,![]() 时,求
时,求![]() 之长.
之长.
【答案】(1)①详见解析;②详见解析;(2)当BE≠DF时,(BE+DF)2+EF2=2AB2仍然成立,理由详见解析;(3)![]()
【解析】
(1)①连接ED、BF,证明四边形BEDF是平行四边形,根据平行四边形的性质证明;②根据正方形的性质、勾股定理证明;
(2)过D作DM⊥BE交BE的延长线于M,连接BD,证明四边形EFDM是矩形,得到EM=DF,DM=EF,∠BMD=90°,根据勾股定理计算;
(3)过P作PE⊥PD,过B作BELPE于E,根据(2)的结论求出PE,结合图形解答.
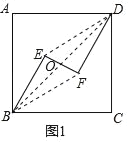
(1)证明:①连接ED、BF,
∵BE∥DF,BE=DF,
∴四边形BEDF是平行四边形,
∴BD、EF互相平分;
②设BD交EF于点O,则OB=OD=![]() BD,OE=OF=
BD,OE=OF=![]() EF.
EF.
∵EF⊥BE,
∴∠BEF=90°.
在Rt△BEO中,BE2+OE2=OB2.
∴(BE+DF)2+EF2=(2BE)2+(2OE)2=4(BE2+OE2)=4OB2=(2OB)2=BD2.
在正方形ABCD中,AB=AD,BD2=AB2+AD2=2AB2.
∴(BE+DF)2+EF2=2AB2;
(2)解:当BE≠DF时,(BE+DF)2+EF2=2AB2仍然成立,
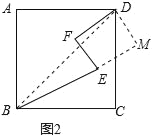
理由如下:如图2,过D作DM⊥BE交BE的延长线于M,连接BD.
∵BE∥DF,EF⊥BE,
∴EF⊥DF,
∴四边形EFDM是矩形,
∴EM=DF,DM=EF,∠BMD=90°,
在Rt△BDM中,BM2+DM2=BD2,
∴(BE+EM)2+DM2=BD2.
即(BE+DF)2+EF2=2AB2;
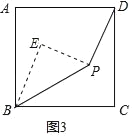
(3)解:过P作PE⊥PD,过B作BE⊥PE于E,
则由上述结论知,(BE+PD)2+PE2=2AB2.
∵∠DPB=135°,
∴∠BPE=45°,
∴∠PBE=45°,
∴BE=PE.
∴△PBE是等腰直角三角形,
∴BP=![]() BE,
BE,
∵![]() BP+2PD=4
BP+2PD=4![]() ,
,
∴2BE+2PD=4![]() ,即BE+PD=2
,即BE+PD=2![]() ,
,
∵AB=4,
∴(2![]() )2+PE2=2×42,
)2+PE2=2×42,
解得,PE=2![]() ,
,
∴BE=2![]() ,
,
∴PD=2![]() ﹣2
﹣2![]() .
.


科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形![]() 中,
中,![]() ,
,![]() ,现将长方形
,现将长方形![]() 向右平移
向右平移![]() ,再向下平移
,再向下平移![]() 后到长方形
后到长方形![]() 的位置.
的位置.
(1)如图,用![]() 的代数式表示长方形
的代数式表示长方形![]() 与长方形
与长方形![]() 的重叠部分的面积,这时
的重叠部分的面积,这时![]() 应满足怎样的条件?
应满足怎样的条件?
(2)如图,用![]() 的代数式表示六边形
的代数式表示六边形![]() 的面积;
的面积;
(3)当这两个长方形没有重叠部分时,第(2)小题的结论是否改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了解学生对四大名著的阅读情况,就“四大古典名著”你读完了几部的问题在全校900名学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
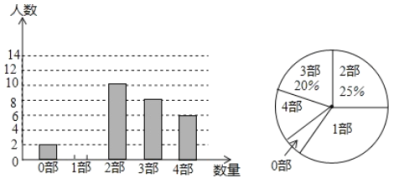
请根据以上信息,解决下列问题
(1)本次调查被调查的学生__________名,学生阅读名著数量(部)的众数是__________,中位数是__________;
(2)扇形统计图中“1部”所在扇形的圆心角为__________度;
(3)请将条形统计图补充完整;
(4)试估算全校大约有多少学生读完了3部以上(含3部)名著.
查看答案和解析>>
科目:初中数学 来源: 题型:
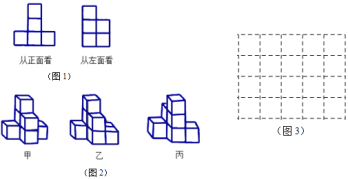
【题目】一个由若干小正方形堆成的几何体,它从正面看和从左面看的图形如图1所示.
![]() 这个几何体可以是图2中甲,乙,丙中的______;
这个几何体可以是图2中甲,乙,丙中的______;
![]() 这个几何体最多由______个小正方体堆成,最少由______个小正方体堆成;
这个几何体最多由______个小正方体堆成,最少由______个小正方体堆成;
![]() 请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形.
请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
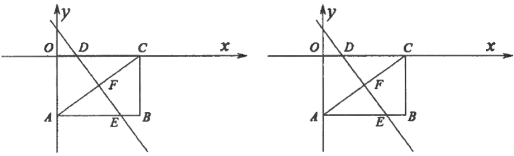
【题目】如图,矩形![]() 的两条边
的两条边![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,已知点
轴上,已知点![]() 坐标为(4,–3).把矩形
坐标为(4,–3).把矩形![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,直线
处,直线![]() 与
与![]() 、
、![]() 、
、![]() 的交点分别为
的交点分别为![]() 、
、![]() 、
、![]() .
.
(1)线段![]() ;
;
(2)求点![]() 坐标及折痕
坐标及折痕![]() 的长;
的长;
(3)若点![]() 在
在![]() 轴上,在平面内是否存在点
轴上,在平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,则请求出点
为顶点的四边形是菱形?若存在,则请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com