
【题目】如图,矩形![]() 的两条边
的两条边![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,已知点
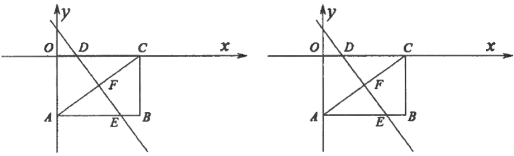
轴上,已知点![]() 坐标为(4,–3).把矩形
坐标为(4,–3).把矩形![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,直线
处,直线![]() 与
与![]() 、
、![]() 、
、![]() 的交点分别为
的交点分别为![]() 、
、![]() 、
、![]() .
.
(1)线段![]() ;
;
(2)求点![]() 坐标及折痕
坐标及折痕![]() 的长;
的长;
(3)若点![]() 在
在![]() 轴上,在平面内是否存在点
轴上,在平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,则请求出点
为顶点的四边形是菱形?若存在,则请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
【答案】(1)![]() ;(2)
;(2)![]() ;拆痕DE的长为
;拆痕DE的长为![]() ; (3)点Q坐标为
; (3)点Q坐标为![]()
【解析】
(1)根据B点的坐标即可求得AC的长度.
(2)首先根据已知条件证明![]() ,再根据相似比例计算DF、CD的长度
,再根据相似比例计算DF、CD的长度
即可计算出D点的坐标,再证明![]() ,根据EF=DF,即可计算的DE的长度.
,根据EF=DF,即可计算的DE的长度.
(3)根据等腰三角形的性质,分类讨论第一种情况当![]() 时;第二种情况当
时;第二种情况当![]() 时;第三种情况当
时;第三种情况当![]() 时,分别计算即可.
时,分别计算即可.
解:(1)![]()
(2)![]() ,由折叠可得:
,由折叠可得:![]()
![]() ,
,![]()
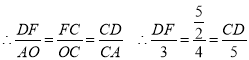 .
.
![]()
![]()
∵四边形OABC是矩形,
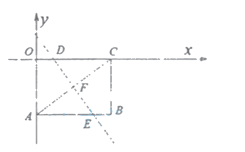
![]()
![]()
![]()
∴拆痕DE的长为![]()
(3)由(2)可知,![]() ,
,
![]()
若以P、D、E、Q为顶点的四边形是菱形,则![]() 必为等腰三角形。
必为等腰三角形。
当![]() 时,可知
时,可知![]() ,
,
此时PE为对角线,可得![]()
当![]() 时,可知
时,可知![]() ,此时DP为对角线,可得
,此时DP为对角线,可得![]() ;
;
当![]() 时,P与C重合,Q与A重合,
时,P与C重合,Q与A重合,![]()
综上所述,满足条件的点Q坐标为![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 是正方形内两点,
是正方形内两点,![]() ,
,![]() ,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程:
,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程:
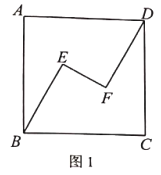
(1)在图1中,连接![]() ,且
,且![]()
①求证:![]() 与
与![]() 互相平分;
互相平分;
②求证:![]() ;
;
(2)在图2中,当![]() ,其它条件不变时,
,其它条件不变时,![]() 是否成立?若成立,请证明:若不成立,请说明理由.
是否成立?若成立,请证明:若不成立,请说明理由.
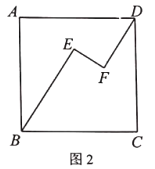
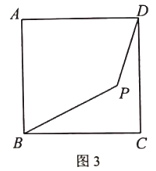
(3)在图3中,当![]() ,
,![]() ,
,![]() 时,求
时,求![]() 之长.
之长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣4ax+3a.
(Ⅰ)求该二次函数的对称轴;
(Ⅱ)若该二次函数的图象开口向下,当1≤x≤4时,y的最大值是2,且当1≤x≤4时,函数图象的最高点为点P,最低点为点Q,求△OPQ的面积;
(Ⅲ)若对于该抛物线上的两点P(x1,y1),Q(x2,y2),当t≤x1≤t+1,x2≥5时,均满足y1≥y2,请结合图象,直接写出t的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作平行四边形ABCD,使∠B=45°,AB=2cm,BC=3cm”的作图过程.
(1)作法:如图,①画∠B=45°;

②在∠B的两边上分别截取BA=2cm,BC=3cm.
③以点A为圆心,BC长为半径画弧,以点![]() 为圆心,AB长为半径画弧,两弧相交于点D;则四边形ABCD为所求的平行四边形.
为圆心,AB长为半径画弧,两弧相交于点D;则四边形ABCD为所求的平行四边形.
根据小东设计的作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵![]() _______,
_______,![]() _______,
_______,
∴四边形ABCD为所求的平行四边形.(____________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克) |
|
|
| 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
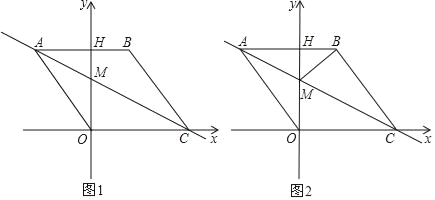
(1)菱形ABCO的边长
(2)求直线AC的解析式;
(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,
①当0<t<![]() 时,求S与t之间的函数关系式;
时,求S与t之间的函数关系式;
②在点P运动过程中,当S=3,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 要了解某公司生产的100万只灯泡的使用寿命,可以采用抽样调查的方法
B. 4位同学的数学期末成绩分别为100、95、105、110,则这四位同学数学期末成绩的中位数为100
C. 甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62
D. 某次抽奖活动中,中奖的概率为![]() 表示每抽奖50次就有一次中奖
表示每抽奖50次就有一次中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装店10月份以每套500元的进价购进一批羽绒服,当月以标价销售,销售额14000元,进入11月份搞促销活动,每件降价50元,这样销售额比10月份增加了5500元,售出的件数是10月份的1.5倍.
(1)求每件羽绒服的标价是多少元;
(2)进入12月份,该服装店决定把剩余的羽绒服按10月份标价的八折销售,结果全部卖掉,而且这批羽绒服总获利不少于12700元,问这批羽绒服至少购进多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+c的图象开口向上,且经过点A(0,![]() ).
).
(1)若此函数的图象经过点(1,0)、(3,0),求此函数的表达式;
(2)若此函数的图象经过点B(2,﹣![]() ),且与x轴交于点C、D.
),且与x轴交于点C、D.
①填空:b=_____(用含α的代数式表示);
②当CD2的值最小时,求此函数的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com