
【题目】在平面直角坐标系中,二次函数y=ax2+bx+c的图象开口向上,且经过点A(0,![]() ).
).
(1)若此函数的图象经过点(1,0)、(3,0),求此函数的表达式;
(2)若此函数的图象经过点B(2,﹣![]() ),且与x轴交于点C、D.
),且与x轴交于点C、D.
①填空:b=_____(用含α的代数式表示);
②当CD2的值最小时,求此函数的表达式.
科目:初中数学 来源: 题型:
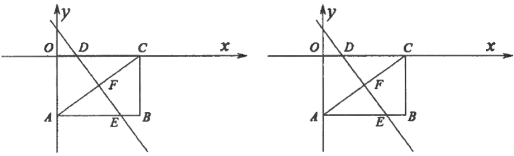
【题目】如图,矩形![]() 的两条边
的两条边![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,已知点
轴上,已知点![]() 坐标为(4,–3).把矩形
坐标为(4,–3).把矩形![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,直线
处,直线![]() 与
与![]() 、
、![]() 、
、![]() 的交点分别为
的交点分别为![]() 、
、![]() 、
、![]() .
.
(1)线段![]() ;
;
(2)求点![]() 坐标及折痕
坐标及折痕![]() 的长;
的长;
(3)若点![]() 在
在![]() 轴上,在平面内是否存在点
轴上,在平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,则请求出点
为顶点的四边形是菱形?若存在,则请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知M、N直线l上两点,MN=20,O、P为线段MN上两动点,过O、P分别作长方形OABC与长方形PDEF(如图),其中,两边OA、PF分别在直线l上,图形在直线l的同侧,且OA=PF=4,CO=DP=3,动点O从点M出发,以1单位/秒的速度向右运动;同时,动点P从点N出发,以2单位/秒的速度向左运动,设运动的时间为t秒.
(1)若t=2.5秒,求点A与点F的距离;
(2)求当t为何值时,两长方形重叠部分为正方形;
(3)运动过程中,在两长方形没有重叠部分前,若能使线段AB、BC、AF的长构成三角形,求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
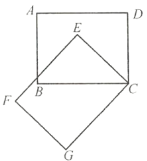
【题目】如图,长方形![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 后得到图形
后得到图形![]() .请回答下列问题:
.请回答下列问题:
(1)点![]() 的对应点是点______,线段
的对应点是点______,线段![]() 的对应线段是______,
的对应线段是______,![]() 的对应角是______;
的对应角是______;
(2)旋转中心是______,![]() 的大小是______,四边形
的大小是______,四边形![]() 的形状是______;
的形状是______;
(3)与线段![]() 相等的线段有______.
相等的线段有______.
查看答案和解析>>
科目:初中数学 来源: 题型:
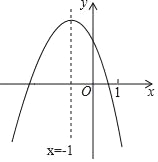
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
①4a+c<0;②m(am+b)+b>a(m≠﹣1);③关于x的一元二次方程ax2+(b﹣1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E.过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为8,∠CDF=22.5°,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读后,请解答.
已知![]() ,符合
,符合![]() 表示大于或等于
表示大于或等于![]() 的最小正整数,如
的最小正整数,如![]() ,
,![]() ,
,![]() ,….
,….
⑴填空:![]() ________,
________,![]() ________,若
________,若![]() ,则
,则![]() 的取值范围是________.
的取值范围是________.
⑵某市的出租车收费标准规定如下:![]() 以内(包括
以内(包括![]() )收费
)收费![]() 元,超过
元,超过![]() 的每超过
的每超过![]() ,加收
,加收![]() 元(不足
元(不足![]() 的按
的按![]() 计算).用
计算).用![]() 表示所行的千米数,
表示所行的千米数,![]() 表示行
表示行![]() 应付车费,则乘车费可按如下的公式计算:当
应付车费,则乘车费可按如下的公式计算:当![]() <
<![]() ≤
≤![]() (单位:
(单位:![]() )时,
)时,![]() (元);当
(元);当![]() (单位:
(单位:![]() )时,
)时,![]() (元).某乘客乘车后付费
(元).某乘客乘车后付费![]() 元,该乘客所行的路程
元,该乘客所行的路程![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店有一台不准确的天平(其臂长不等)及![]() 砝码.某顾客要购买
砝码.某顾客要购买![]() 糖果,售货员先将砝码放于左盘,置一些糖果于右盘,使之平衡后给顾客;又将
糖果,售货员先将砝码放于左盘,置一些糖果于右盘,使之平衡后给顾客;又将![]() 砝码放于右盘,另置糖果于左盘,平衡后再倒给顾客,这种称法是否合理?[提示:当天平(不准确)平衡后,所挂重物与臂长成反比].
砝码放于右盘,另置糖果于左盘,平衡后再倒给顾客,这种称法是否合理?[提示:当天平(不准确)平衡后,所挂重物与臂长成反比].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com