
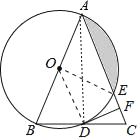
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E.过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为8,∠CDF=22.5°,求阴影部分的面积.

【答案】(1)证明见解析;(2)S阴影= 16π﹣32.
【解析】试题分析:
(1)连接OD,AD,由AB是⊙O的直径可得∠ADB=90°,结合AB=AC可得点D是BC的中点,结合点O是AB中点可得OD是△ABC的中位线,由此可得OD∥AC,结合DF⊥AC即可得到DF⊥OD,由此可得DF是⊙O的切线;
(2)连接OE,由DF⊥AC于点F结合∠CDF=22.5°可得∠C=67.5°,这样结合AB=AC可得∠B=67.5°,从而可得∠BAC=45°,再结合AO=EO即可得到∠AOE=90°,这样就可由S阴影=S扇形AOE-S△AOE求出S阴影的大小了.
试题解析:
(1)连接OD,AD.
∵AB是⊙O的直径,
∴∠ADB=90°,
∵AB=AC,∠ADB=90°,
∴BD=CD,
∵AO=BO,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴半径OD⊥DF,
∴DF是⊙O的切线.
(2)连接OE.
∵DF⊥AC,∠CDF=22.5°,
∴∠C=67.5°,
∵AB=AC,
∴∠C=∠B=67.5°,
∴∠BAC=45°,
∵OA=OE,
∴∠AOE=90°,
又∵⊙O的半径为8,
∴S阴影=S扇形AOE﹣S△AOE=16π﹣32.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 要了解某公司生产的100万只灯泡的使用寿命,可以采用抽样调查的方法
B. 4位同学的数学期末成绩分别为100、95、105、110,则这四位同学数学期末成绩的中位数为100
C. 甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62
D. 某次抽奖活动中,中奖的概率为![]() 表示每抽奖50次就有一次中奖
表示每抽奖50次就有一次中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,
①四边形![]() 是平行四边形;
是平行四边形;
②![]() 是等腰三角形;
是等腰三角形;
③四边形![]() 的周长是
的周长是![]() ;
;
④四边形![]() 的面积是16.
的面积是16.
则以上结论正确的是![]()
![]()

A. ①②③B. ①②④C. ①③④D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+c的图象开口向上,且经过点A(0,![]() ).
).
(1)若此函数的图象经过点(1,0)、(3,0),求此函数的表达式;
(2)若此函数的图象经过点B(2,﹣![]() ),且与x轴交于点C、D.
),且与x轴交于点C、D.
①填空:b=_____(用含α的代数式表示);
②当CD2的值最小时,求此函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简、在求值:
(1)(4a2-3a)-(1-4a+4a2),其中a=-2
(2)有8个算式,排成4行2列
2+2,2×2
3+![]() ,3×
,3×![]()
4+![]() ,4×
,4×![]()
5+![]() ,5×
,5×![]()
①同一行中两个算式的结果怎样?
②算式2019+![]() 和2019×
和2019×![]() 的结果相等吗?
的结果相等吗?
③请你写出算式,试一试,再探索其规律,用含自然数n的代数式表示这一规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
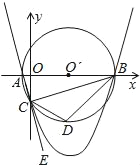
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC,BC,过A,B,C三点作抛物线.
(1)求抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连接BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.
第三问改成,在(2)的条件下,点P是直线BC下方的抛物线上一动点,当点P运动到什么位置时,△PCD的面积是△BCD面积的三分之一,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
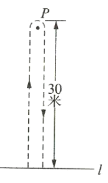
【题目】甲、乙两同学玩“托球赛跑”游戏,商定:用球拍托着乒乓球从起跑线![]() 起跑,绕过
起跑,绕过![]() 点跑回到起跑线(如图所示);途中乒乓球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果甲同学由于心急掉了球,浪费了6秒钟,乙同学则顺利跑完.事后,甲同学说我俩所用的全部时间的和为50秒”,乙同学说捡球过程不算在内时,甲的速度是我的1.2倍.”根据图文信息,请问甲同学的速度是______米/秒.
点跑回到起跑线(如图所示);途中乒乓球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果甲同学由于心急掉了球,浪费了6秒钟,乙同学则顺利跑完.事后,甲同学说我俩所用的全部时间的和为50秒”,乙同学说捡球过程不算在内时,甲的速度是我的1.2倍.”根据图文信息,请问甲同学的速度是______米/秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C为数轴上的三点,动点A、B同时从原点出发,动点A每秒运动x个单位,动点B每秒运动y个单位,且动点A运动到的位置对应的数记为a,动点B运动到的位置对应的数记为b,定点C对应的数为8.
(1)若2秒后,a、b满足|a+8|+|b﹣2|=0,则x= ,y= .并请在数轴上标出A、B两点的位置.
(2)若动点A、B在(1)运动后的位置上保持原来的速度,且同时向正方向运动z秒后使得|a|=|b|,使得z= .
(3)若动点A、B在(1)运动后的位置上都以每秒2个单位向正方向运动继续运动t秒,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,点A与点B之间的距离为AB,且AC+BC=1.5AB,则t= .
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com