
ЁОЬтФПЁПAЁЂBЁЂCЮЊЪ§жсЩЯЕФШ§ЕуЃЌЖЏЕуAЁЂBЭЌЪБДгдЕуГіЗЂЃЌЖЏЕуAУПУыдЫЖЏxИіЕЅЮЛЃЌЖЏЕуBУПУыдЫЖЏyИіЕЅЮЛЃЌЧвЖЏЕуAдЫЖЏЕНЕФЮЛжУЖдгІЕФЪ§МЧЮЊaЃЌЖЏЕуBдЫЖЏЕНЕФЮЛжУЖдгІЕФЪ§МЧЮЊbЃЌЖЈЕуCЖдгІЕФЪ§ЮЊ8ЃЎ
ЃЈ1ЃЉШє2УыКѓЃЌaЁЂbТњзу|a+8|+|bЉ2|ЃН0ЃЌдђxЃНЁЁ ЁЁЃЌyЃНЁЁ ЁЁЃЎВЂЧыдкЪ§жсЩЯБъГіAЁЂBСНЕуЕФЮЛжУЃЎ
ЃЈ2ЃЉШєЖЏЕуAЁЂBдкЃЈ1ЃЉдЫЖЏКѓЕФЮЛжУЩЯБЃГждРДЕФЫйЖШЃЌЧвЭЌЪБЯђе§ЗНЯђдЫЖЏzУыКѓЪЙЕУ|a|ЃН|b|ЃЌЪЙЕУzЃНЁЁ ЁЁЃЎ
ЃЈ3ЃЉШєЖЏЕуAЁЂBдкЃЈ1ЃЉдЫЖЏКѓЕФЮЛжУЩЯЖМвдУПУы2ИіЕЅЮЛЯђе§ЗНЯђдЫЖЏМЬајдЫЖЏtУыЃЌЕуAгыЕуCжЎМфЕФОрРыБэЪОЮЊACЃЌЕуBгыЕуCжЎМфЕФОрРыБэЪОЮЊBCЃЌЕуAгыЕуBжЎМфЕФОрРыЮЊABЃЌЧвAC+BCЃН1.5ABЃЌдђtЃНЁЁ ЁЁЃЎ
![]()
ЁОД№АИЁПЃЈ1ЃЉ4ЃЌ1ЃЌЭМЯъМћНтЮіЃЛЃЈ2ЃЉ![]() Лђ
Лђ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЁп|a+8|+ЃЈbЉ2ЃЉ2=0ЃЌ
Ёрa+8=0ЃЌbЉ2=0ЃЌМДa=Љ8ЃЌb=2ЃЌ
дђx=|Љ8|ЁТ2=4ЃЌy=2ЁТ2=1ЃЌ
дкЪ§жсЩЯБъГіAЁЂBСНЕуЕФЮЛжУШчЯТЭМЫљЪОЃК
![]()
ЙЪД№АИЮЊЃК4ЃЌ1ЃЛ
ЃЈ2ЃЉЁпЖЏЕуAЁЂBдкЃЈ1ЃЉдЫЖЏКѓЕФЮЛжУЩЯБЃГждРДЕФЫйЖШЃЌЧвЭЌЪБЯђе§ЗНЯђдЫЖЏzУыКѓЃЌ
Ёрa=Љ8+4zЃЌb=2+zЃЎ
Ёп|a|=|b|ЃЌ
Ёр|Љ8+4z|=|2+z|ЃЌ
ЁрЉ8+4z+2+z=0ЛђЉ8+4z=2+z
НтЕУЃКz=![]() Лђz=
Лђz=![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШєЖЏЕуAЁЂBдкЃЈ1ЃЉдЫЖЏКѓЕФЮЛжУЩЯЖМвдУПУы2ИіЕЅЮЛЯђе§ЗНЯђдЫЖЏМЬајдЫЖЏtУыКѓЃЌ
дђЕуAБэЪОЃКЉ8+2tЃЌЕуBБэЪОЃК2+2tЃЌЕуCБэЪОЃК8ЃЌ
ЁрAC=|Љ8+2tЉ8|=|2tЉ16|ЃЌBC=|2+2tЉ8|=|2tЉ6|ЃЌAB=|Љ8+2tЉЃЈ2+2tЃЉ|=10ЃЎ
ЁпAC+BC=1.5ABЃЌ
Ёр|2tЉ16|+|2tЉ6|=1.5ЁС10ЃЌ
ЗжШ§жжЧщПіЬжТлЃК
ЂйЕБtЁм3ЪБЃЌ
16-2t+6-2t=15ЃЌ
НтЕУЃКt=![]() ЃЛ
ЃЛ
ЂкЕБ3ЃМtЁм8ЪБЃЌ
16-2t+2t-6=10Ёй15
ЗНГЬЮоНтЃЛ
ЂлЕБtЃО8ЪБЃЌ
2t-16+2t-6=15
НтЕУЃКt=![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃКt=![]() Лђt=
Лђt=![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК![]() Лђ
Лђ ![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌвдABЮЊжБОЖЕФЁбOЗжБ№гыBCЃЌACНЛгкЕуDЃЌEЃЎЙ§ЕуDзїDFЁЭACНЛACгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКDFЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ8ЃЌЁЯCDF=22.5ЁуЃЌЧѓвѕгАВПЗжЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЪ§жсЩЯгаAЁЂBЁЂCЁЂDЫФИіЕуЃЌЧвЯпЖЮAB=4ЃЌCD=6ЃЌвбжЊAБэЪОЕФЪ§ЪЧЉ10ЃЌCБэЪОЕФЪ§ЪЧ8ЃЌШєЯпЖЮABвдУПУы6ИіЕЅЮЛГЄЖШЕФЫйЖШЃЌЯпЖЮCDвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШдкЪ§жсЩЯдЫЖЏЃЈAдкBзѓВрЃЌCдкDзѓВрЃЉ
ЃЈ1ЃЉBЃЌDСНЕуЫљБэЪОЕФЪ§ЗжБ№ЪЧЁЁ ЁЁЁЂЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєЯпЖЮABЯђгвдЫЖЏЃЌЭЌЪБЯпЖЮCDЯђзѓдЫЖЏЃЌОЙ§ЖрЩйУыЪБЃЌBC=2ЃЛ
ЃЈ3ЃЉШєЯпЖЮABЁЂCDЭЌЪБЯђгвдЫЖЏЃЌЭЌЪБЕуPДгдЕуГіЗЂвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђгвдЫЖЏЃЌОЙ§ЖрЩйУыЪБЃЌЕуPЕНЕуAЃЌCЕФОрРыЯрЕШЃП
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъгавЛЬЈВЛзМШЗЕФЬьЦНЃЈЦфБлГЄВЛЕШЃЉМА![]() эРТы.ФГЙЫПЭвЊЙКТђ
эРТы.ФГЙЫПЭвЊЙКТђ![]() ЬЧЙћЃЌЪлЛѕдБЯШНЋэРТыЗХгкзѓХЬЃЌжУвЛаЉЬЧЙћгкгвХЬЃЌЪЙжЎЦНКтКѓИјЙЫПЭЃЛгжНЋ
ЬЧЙћЃЌЪлЛѕдБЯШНЋэРТыЗХгкзѓХЬЃЌжУвЛаЉЬЧЙћгкгвХЬЃЌЪЙжЎЦНКтКѓИјЙЫПЭЃЛгжНЋ![]() эРТыЗХгкгвХЬЃЌСэжУЬЧЙћгкзѓХЬЃЌЦНКтКѓдйЕЙИјЙЫПЭЃЌетжжГЦЗЈЪЧЗёКЯРэЃП[ЬсЪОЃКЕБЬьЦНЃЈВЛзМШЗЃЉЦНКтКѓЃЌЫљЙвжиЮягыБлГЄГЩЗДБШ].
эРТыЗХгкгвХЬЃЌСэжУЬЧЙћгкзѓХЬЃЌЦНКтКѓдйЕЙИјЙЫПЭЃЌетжжГЦЗЈЪЧЗёКЯРэЃП[ЬсЪОЃКЕБЬьЦНЃЈВЛзМШЗЃЉЦНКтКѓЃЌЫљЙвжиЮягыБлГЄГЩЗДБШ].
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
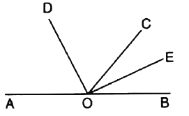
ЁОЬтФПЁПШчЭМ,ЕуAЁЂBдкЭЌвЛЬѕжБЯпЩЯ,ODЁЂOEЗжБ№ЦНЗжЁЯAOCКЭЁЯBOC.(1)ЧѓЁЯDOEЕФЖШЪ§ЃЛ(2)ШчЙћЁЯCOD=65Ёу,ЧѓЁЯAOEЕФЖШЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЯыСЫНтбЇЩњУПжмЕФПЮЭтдФЖСЪБМфЧщПіЃЌЫцЛњЕїВщСЫВПЗжбЇЩњЃЌЖдбЇЩњУПжмЕФПЮЭтдФЖСЪБМфxЃЈЕЅЮЛЃКаЁЪБЃЉНјааЗжзщећРэЃЌВЂЛцжЦСЫШчЭМЫљЪОЕФВЛЭъећЕФЦЕЪ§ЗжБ№жБЗНЭМКЭЩШаЮЭГМЦЭМЃК

ИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМ
ЃЈ2ЃЉЧѓЩШаЮЭГМЦЭМжаmЕФжЕКЭEзщЖдгІЕФдВаФНЧЖШЪ§
ЃЈ3ЃЉЧыЙРМЦИУаЃ3000УћбЇЩњжаУПжмЕФПЮЭтдФЖСЪБМфВЛаЁгк6аЁЪБЕФШЫЪ§
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉЯШЛЏМђЃЌдйЧѓжЕЃК xЉ2ЃЈxЉ![]() y2ЃЉ+ЃЈЉ2x+
y2ЃЉ+ЃЈЉ2x+![]() y2ЃЉЃЌЦфжаxЃН2ЃЌyЃНЉ3
y2ЃЉЃЌЦфжаxЃН2ЃЌyЃНЉ3
ЃЈ2ЃЉвбжЊЃКШєaЃЌbЛЅЮЊЯрЗДЪ§ЃЌcЃЌdЛЅЮЊЕЙЪ§ЃЌmЕФОјЖджЕЮЊзюаЁе§ећЪ§ЃЌЧѓДњЪ§ЪНЉ2cd+![]() ЉmЕФжЕ
ЉmЕФжЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьвЛзщЪ§ОнЃК2ЃЌ4ЃЌ7ЃЌ11ЃЌ16ЃЌ22ЃЌ29ЃЌЁЃЌЫќУЧгавЛЖЈЕФЙцТЩЃЌШєМЧЕквЛИіЪ§ЮЊa1ЃЌЕкЖўИіЪ§МЧЮЊa2ЃЌЁЃЌЕкnИіЪ§МЧЮЊan.
(1)ЧыаДГі29КѓУцЕФЕквЛИіЪ§ЃЛ
(2)ЭЈЙ§МЦЫуa2Ѓa1ЃЌa3Ѓa2ЃЌa4Ѓa3ЃЌЁгЩДЫЭЦЫуa100Ѓa99ЕФжЕЃЛ
(3)ИљОнФуЗЂЯжЕФЙцТЩЧѓa100ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
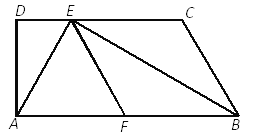
ЁОЬтФПЁПШчЭМЃЌвбжЊЬнаЮABCDжаЃЌABЁЮCDЃЌЁЯD=90ЁуЃЌBEЦНЗжЁЯABCЃЌНЛCDгкЕуEЃЌFЪЧABЕФжаЕуЃЌСЊНсAEЁЂEFЃЌЧвAEЁЭBEЃЎ
ЧѓжЄЃКЃЈ1ЃЉЫФБпаЮBCEFЪЧСтаЮЃЛ
ЃЈ2ЃЉ![]() .
.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com