
����Ŀ���Ķ�������
��֪![]() ������
������![]() ��ʾ���ڻ����
��ʾ���ڻ����![]() ����С����������
��������������![]() ��
��![]() ��
��![]() ������
������
����գ�![]() ________��
________��![]() ________����
________����![]() ����
����![]() ��ȡֵ��Χ��________��
��ȡֵ��Χ��________��
��ij�еij���շѱ��涨���£�![]() ����(����
����(����![]() )�շ�
)�շ�![]() Ԫ������
Ԫ������![]() ��ÿ����
��ÿ����![]() ������
������![]() Ԫ(����
Ԫ(����![]() �İ�
��![]() ����)����
����)����![]() ��ʾ���е�ǧ������
��ʾ���е�ǧ������![]() ��ʾ��
��ʾ��![]() Ӧ�����ѣ���˳��ѿɰ����µĹ�ʽ���㣺��
Ӧ�����ѣ���˳��ѿɰ����µĹ�ʽ���㣺��![]() ��
��![]() ��
��![]() (���
(��λ��![]() )ʱ��
)ʱ��![]() (Ԫ)����
(Ԫ)����![]() (��λ��
(��λ��![]() )ʱ��
)ʱ��![]() (Ԫ)��ij�˿ͳ˳���
(Ԫ)��ij�˿ͳ˳���![]() Ԫ���ó˿����е�·��
Ԫ���ó˿����е�·��![]() ��ȡֵ��Χ��________��
��ȡֵ��Χ��________��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����װ��10�·���ÿ��500Ԫ�Ľ��۹���һ�������������Ա�����ۣ����۶�14000Ԫ������11�·ݸ�������ÿ������50Ԫ���������۶��10�·�������5500Ԫ���۳��ļ�����10�·ݵ�1.5����
��1����ÿ�������ı���Ƕ���Ԫ��
��2������12�·ݣ��÷�װ�������ʣ���������10�·ݱ�۵İ������ۣ����ȫ���������������������ܻ���������12700Ԫ���������������ٹ������ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����κ���y=ax2+bx+c��ͼ�����ϣ��Ҿ�����A��0��![]() ����
����
��1�����˺�����ͼ���㣨1��0������3��0������˺����ı���ʽ��
��2�����˺�����ͼ����B��2����![]() ��������x�ύ�ڵ�C��D��
��������x�ύ�ڵ�C��D��
����գ�b=_____���ú����Ĵ���ʽ��ʾ����
�ڵ�CD2��ֵ��Сʱ����˺����ı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
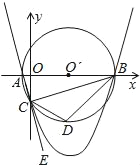
����Ŀ����ͼ����֪��A�������ǣ���1��0������B�������ǣ�9��0������ABΪֱ������O������y��ĸ������ڵ�C������AC��BC����A��B��C�����������ߣ�
��1���������ߵĽ���ʽ��
��2����E��AC�ӳ�����һ�㣬��BCE��ƽ����CD����O���ڵ�D������BD����ֱ��BD�Ľ���ʽ��
��3���ڣ�2���������£����������Ƿ���ڵ�P��ʹ�á�PDB=��CBD��������ڣ��������P�����ꣻ��������ڣ���˵�����ɣ�
�����ʸijɣ��ڣ�2���������£���P��ֱ��BC�·�����������һ���㣬����P�˶���ʲôλ��ʱ����PCD���������BCD���������֮һ�����ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
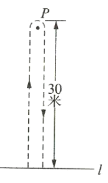
����Ŀ���ס�����ͬѧ�桰�������ܡ���Ϸ���̶�������������ƹ�����������![]() ���ܣ��ƹ�
���ܣ��ƹ�![]() ���ܻص������ߣ���ͼ��ʾ����;��ƹ�������ʱ����ص����������ܣ���ʱ����ʤ.�����ͬѧ�����ļ��������˷���6���ӣ���ͬѧ��˳������.�º�ͬѧ˵�������õ�ȫ��ʱ��ĺ�Ϊ50�롱����ͬѧ˵������̲�������ʱ�����ٶ����ҵ�1.2��.������ͼ����Ϣ�����ʼ�ͬѧ���ٶ���______��/��.
���ܻص������ߣ���ͼ��ʾ����;��ƹ�������ʱ����ص����������ܣ���ʱ����ʤ.�����ͬѧ�����ļ��������˷���6���ӣ���ͬѧ��˳������.�º�ͬѧ˵�������õ�ȫ��ʱ��ĺ�Ϊ50�롱����ͬѧ˵������̲�������ʱ�����ٶ����ҵ�1.2��.������ͼ����Ϣ�����ʼ�ͬѧ���ٶ���______��/��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����O��ֱ��AB=12��P����BC��һ���㣨���B��C���غϣ�����ABC=30�㣬����P��PD��OP����O�ڵ�D��
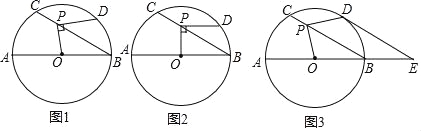
��1����ͼ2����PD��ABʱ����PD�ij���
��2����ͼ3����![]() ʱ���ӳ�AB����E��ʹBE=
ʱ���ӳ�AB����E��ʹBE=![]() AB������DE��
AB������DE��
����֤��DE����O�����ߣ�
����PC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ԡ�AOB�Ķ���OΪ�˵�������OP��ʹ��AOP����BOP=3��2������AOB=20�������AOP�Ķ���Ϊ_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�죬һ�߲˾�Ӫ����90ԪǮ�������۴��߲������г������������Ͷ��ǹ�50kg��Ȼ�����г��ϰ����ۼ۳��ۣ��������Ͷ��ǵ���������ۺ����ۼ����±���ʾ��
Ʒ�� | ������ | ���� |
�����ۣ���λ��Ԫ/kg�� | 2.0 | 1.5 |
���ۼۣ���λ��Ԫ/kg�� | 2.9 | 2.6 |
����������Ͷ���ȫ�������ۼ��۳�������������Щ�������Ͷ����˶���ԪǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
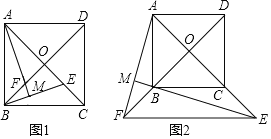
����Ŀ��������ABCD�ĶԽ���AC��BD���ڵ�O����E��F�ֱ���OC��OB�ϣ���OE=OF��
��1����ͼ1������E��F���߶�OC��OB�ϣ�����AF���ӳ���BE�ڵ�M����֤��AM��BE��
��2����ͼ2������E��F���߶�OC��OB���ӳ����ϣ�����EB���ӳ���AF�ڵ�M��
�١�AME�Ķ���Ϊ ��
����������ABCD�ı߳�Ϊ3![]() ����OC=3CEʱ����BM�ij���
����OC=3CEʱ����BM�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com