
【题目】如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
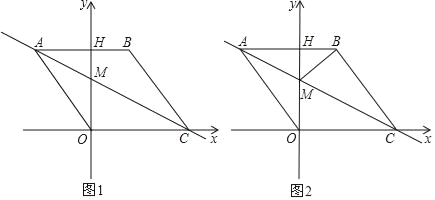
(1)菱形ABCO的边长
(2)求直线AC的解析式;
(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,
①当0<t<![]() 时,求S与t之间的函数关系式;
时,求S与t之间的函数关系式;
②在点P运动过程中,当S=3,请直接写出t的值.
【答案】(1)5;(2)直线AC的解析式y=﹣![]() x+
x+![]() ;(3)见解析.
;(3)见解析.
【解析】分析:(1)Rt△AOH中利用勾股定理即可求得菱形的边长;
(2)根据(1)即可求的OC的长,则C的坐标即可求得,利用待定系数法即可求得直线AC的解析式;
(3)根据S△ABC=S△AMB+S△BMC求得M到直线BC的距离为h,然后分成P在AM上和在MC上两种情况讨论,利用三角形的面积公式求解.
详解:(1)Rt△AOH中,
AO=![]() =
=![]() =5,
=5,
所以菱形边长为5;
故答案为:5;
(2)∵四边形ABCO是菱形,
∴OC=OA=AB=5,即C(5,0).
设直线AC的解析式y=kx+b,函数图象过点A、C,得
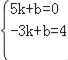 ,解得
,解得![]() ,
,
直线AC的解析式y=﹣![]() x+
x+![]() ;
;
(3)设M到直线BC的距离为h,
当x=0时,y=![]() ,即M(0,
,即M(0,![]() ),HM=HO﹣OM=4﹣
),HM=HO﹣OM=4﹣![]() =
=![]() ,
,
由S△ABC=S△AMB+SBMC=![]() ABOH=
ABOH=![]() ABHM+
ABHM+![]() BCh,
BCh,
![]() ×5×4=
×5×4=![]() ×5×
×5×![]() +
+![]() ×5h,解得h=
×5h,解得h=![]() ,
,
①当0<t<![]() 时,BP=BA﹣AP=5﹣2t,HM=OH﹣OM=
时,BP=BA﹣AP=5﹣2t,HM=OH﹣OM=,
S=![]() BPHM=
BPHM=![]() ×
×![]() (5﹣2t)=﹣
(5﹣2t)=﹣![]() t+
t+![]() ;
;
②当2.5<t≤5时,BP=2t﹣5,h=![]() ,
,
S=![]() BPh=
BPh=![]() ×
×![]() (2t﹣5)=
(2t﹣5)=![]() t﹣
t﹣![]() ,
,
把S=3代入①中的函数解析式得,3=﹣![]() t+
t+![]() ,
,
解得:t=![]() ,
,
把S=3代入②的解析式得,3=![]() t﹣
t﹣![]() ,
,
解得:t=![]() .
.
∴t=![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了解学生对四大名著的阅读情况,就“四大古典名著”你读完了几部的问题在全校900名学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
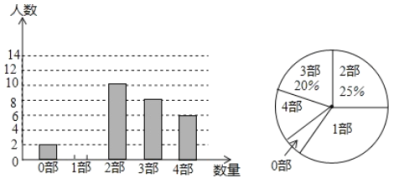
请根据以上信息,解决下列问题
(1)本次调查被调查的学生__________名,学生阅读名著数量(部)的众数是__________,中位数是__________;
(2)扇形统计图中“1部”所在扇形的圆心角为__________度;
(3)请将条形统计图补充完整;
(4)试估算全校大约有多少学生读完了3部以上(含3部)名著.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,A, B是直线l上的两点,点B关于AD的对称点为M,连接![]() 交AD于F点.
交AD于F点.
(1)若![]() ,如图,
,如图,
①依题意补全图形;
②判断MF与FC的数量关系是 ;

(2)如图,当![]() 时,
时,![]() ,CD的延长线相交于点E,取
,CD的延长线相交于点E,取![]() E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.
E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的两条边
的两条边![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,已知点
轴上,已知点![]() 坐标为(4,–3).把矩形
坐标为(4,–3).把矩形![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,直线
处,直线![]() 与
与![]() 、
、![]() 、
、![]() 的交点分别为
的交点分别为![]() 、
、![]() 、
、![]() .
.
(1)线段![]() ;
;
(2)求点![]() 坐标及折痕
坐标及折痕![]() 的长;
的长;
(3)若点![]() 在
在![]() 轴上,在平面内是否存在点
轴上,在平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,则请求出点
为顶点的四边形是菱形?若存在,则请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
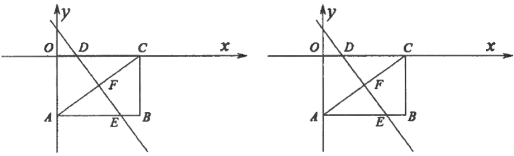
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.

(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
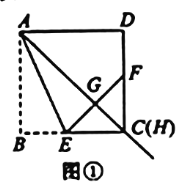
【题目】在正方形![]() 中,过点A引射线
中,过点A引射线![]() ,交边
,交边![]() 于点H(H不与点D重合).通过翻折,使点B落在射线
于点H(H不与点D重合).通过翻折,使点B落在射线![]() 上的点G处,折痕
上的点G处,折痕![]() 交
交![]() 于E,连接E,G并延长
于E,连接E,G并延长![]() 交
交![]() 于F.
于F.
(1)如图1,当点H与点C重合时,![]() 与
与![]() 的大小关系是_________;
的大小关系是_________;![]() 是____________三角形.
是____________三角形.
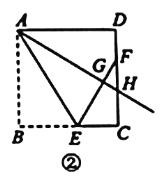
(2)如图2,当点H为边![]() 上任意一点时(点H与点C不重合).连接
上任意一点时(点H与点C不重合).连接![]() ,猜想
,猜想![]() 与
与![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
(3)在图2,当![]() ,
,![]() 时,求
时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果2b=n,那么称b为n的布谷数,记为b=g(n),如g(8)=g(23)=3.
(1)根据布谷数的定义填空:g(2)= ,g(32)= .
(2)布谷数有如下运算性质:若m,n为正数,则g(mn)=g(m)+g(n),g(![]() )=g(m)﹣g(n).根据运算性质填空:
)=g(m)﹣g(n).根据运算性质填空:![]() = ,(a为正数).若g(7)=2.807,则g(14)= ,g(
= ,(a为正数).若g(7)=2.807,则g(14)= ,g(![]() )= .
)= .
(3)下表中与数x对应的布谷数g(x)有且仅有两个是错误的,请指出错误的布谷数,要求说明你这样找的理由,并求出正确的答案(用含a,b的代数式表示)
x |
|
| 3 | 6 | 9 | 27 |
g(x) | 1﹣4a+2b | 1﹣2a+b | 2a﹣b | 3a﹣2b | 4a﹣2b | 6a﹣3b |
查看答案和解析>>
科目:初中数学 来源: 题型:
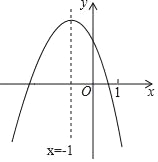
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
①4a+c<0;②m(am+b)+b>a(m≠﹣1);③关于x的一元二次方程ax2+(b﹣1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com