
【题目】在正方形![]() 中,过点A引射线
中,过点A引射线![]() ,交边
,交边![]() 于点H(H不与点D重合).通过翻折,使点B落在射线
于点H(H不与点D重合).通过翻折,使点B落在射线![]() 上的点G处,折痕
上的点G处,折痕![]() 交
交![]() 于E,连接E,G并延长
于E,连接E,G并延长![]() 交
交![]() 于F.
于F.
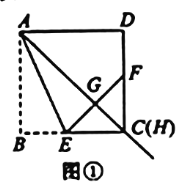
(1)如图1,当点H与点C重合时,![]() 与
与![]() 的大小关系是_________;
的大小关系是_________;![]() 是____________三角形.
是____________三角形.
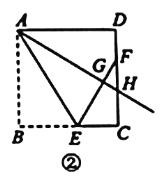
(2)如图2,当点H为边![]() 上任意一点时(点H与点C不重合).连接
上任意一点时(点H与点C不重合).连接![]() ,猜想
,猜想![]() 与
与![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
(3)在图2,当![]() ,
,![]() 时,求
时,求![]() 的面积.
的面积.
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角项点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.

(1)将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周.如图2,经过t秒后,ON落在OC边上,则t= 秒(直接写结果).
(2)在(1)的条件下,若三角板继续转动,同时射线OC也绕O点以每秒10°的速度沿逆时针方向旋转一周,当OC转动9秒时,求∠MOC的度数.
(3)在(2)的条件下,它们继续运动多少秒时,∠MOC=35°?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作平行四边形ABCD,使∠B=45°,AB=2cm,BC=3cm”的作图过程.
(1)作法:如图,①画∠B=45°;

②在∠B的两边上分别截取BA=2cm,BC=3cm.
③以点A为圆心,BC长为半径画弧,以点![]() 为圆心,AB长为半径画弧,两弧相交于点D;则四边形ABCD为所求的平行四边形.
为圆心,AB长为半径画弧,两弧相交于点D;则四边形ABCD为所求的平行四边形.
根据小东设计的作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵![]() _______,
_______,![]() _______,
_______,
∴四边形ABCD为所求的平行四边形.(____________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
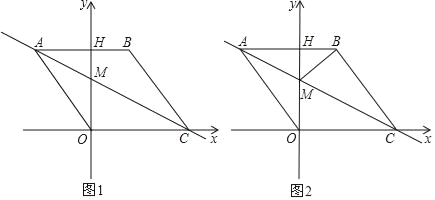
(1)菱形ABCO的边长
(2)求直线AC的解析式;
(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,
①当0<t<![]() 时,求S与t之间的函数关系式;
时,求S与t之间的函数关系式;
②在点P运动过程中,当S=3,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 要了解某公司生产的100万只灯泡的使用寿命,可以采用抽样调查的方法
B. 4位同学的数学期末成绩分别为100、95、105、110,则这四位同学数学期末成绩的中位数为100
C. 甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62
D. 某次抽奖活动中,中奖的概率为![]() 表示每抽奖50次就有一次中奖
表示每抽奖50次就有一次中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年6月11日至17日是我国第29个全国节能宣传周,主题为“节能减耗,保卫蓝天”。某学校为配合宣传活动,抽查了某班级10天的用电量,数据如下表(单位:度):
度数 | 8 | 9 | 10 | 13 | 14 | 15 |
天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(1)这10天用电量的众数是___________,中位数是_________;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级,试估计该校6月份(30天)总的用电量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装店10月份以每套500元的进价购进一批羽绒服,当月以标价销售,销售额14000元,进入11月份搞促销活动,每件降价50元,这样销售额比10月份增加了5500元,售出的件数是10月份的1.5倍.
(1)求每件羽绒服的标价是多少元;
(2)进入12月份,该服装店决定把剩余的羽绒服按10月份标价的八折销售,结果全部卖掉,而且这批羽绒服总获利不少于12700元,问这批羽绒服至少购进多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
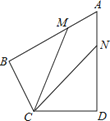
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=
查看答案和解析>>
科目:初中数学 来源: 题型:
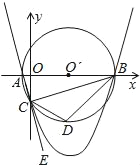
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC,BC,过A,B,C三点作抛物线.
(1)求抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连接BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.
第三问改成,在(2)的条件下,点P是直线BC下方的抛物线上一动点,当点P运动到什么位置时,△PCD的面积是△BCD面积的三分之一,求此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com