
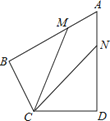
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=
【答案】![]()
【解析】试题分析:连接AC,通过三角形全等,求得∠BAC=30°,从而求得BC的长,然后根据勾股定理求得CM的长,连接MN,过M点作ME⊥CN于E,则△MNA是等边三角形求得MN=2,设NE=x,表示出CE,根据勾股定理即可求得ME,然后求得tan∠MCN.
试题解析:∵AB=AD=6,AM:MB=AN:ND=1:2,
∴AM=AN=2,BM=DN=4,
连接MN,连接AC,
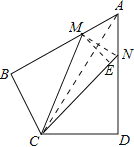
∵AB⊥BC,AD⊥CD,∠BAD=60°
在Rt△ABC与Rt△ADC中,
![]() ,
,
∴Rt△ABC≌Rt△ADC(HL)
∴∠BAC=∠DAC=![]() ∠BAD=30°,MC=NC,
∠BAD=30°,MC=NC,
∴BC=![]() AC,
AC,
∴AC2=BC2+AB2,即(2BC)2=BC2+AB2,
3BC2=AB2,
∴BC=2![]() ,
,
在Rt△BMC中,CM=![]()
∵AN=AM,∠MAN=60°,
∴△MAN是等边三角形,
∴MN=AM=AN=2,
过M点作ME⊥CN于E,设NE=x,则CE=2![]() -x,
-x,
∴MN2-NE2=MC2-EC2,即4-x2=(2![]() )2-(2
)2-(2![]() -x)2,
-x)2,
解得:x=![]() ,
,
∴EC=2![]() -
-![]() =
=![]() ,
,
∴ME=![]() ,
,
∴tan∠MCN=![]() .
.


科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,过点A引射线
中,过点A引射线![]() ,交边
,交边![]() 于点H(H不与点D重合).通过翻折,使点B落在射线
于点H(H不与点D重合).通过翻折,使点B落在射线![]() 上的点G处,折痕
上的点G处,折痕![]() 交
交![]() 于E,连接E,G并延长
于E,连接E,G并延长![]() 交
交![]() 于F.
于F.
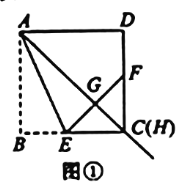
(1)如图1,当点H与点C重合时,![]() 与
与![]() 的大小关系是_________;
的大小关系是_________;![]() 是____________三角形.
是____________三角形.
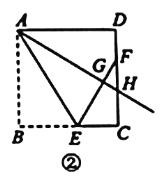
(2)如图2,当点H为边![]() 上任意一点时(点H与点C不重合).连接
上任意一点时(点H与点C不重合).连接![]() ,猜想
,猜想![]() 与
与![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
(3)在图2,当![]() ,
,![]() 时,求
时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果2b=n,那么称b为n的布谷数,记为b=g(n),如g(8)=g(23)=3.
(1)根据布谷数的定义填空:g(2)= ,g(32)= .
(2)布谷数有如下运算性质:若m,n为正数,则g(mn)=g(m)+g(n),g(![]() )=g(m)﹣g(n).根据运算性质填空:
)=g(m)﹣g(n).根据运算性质填空:![]() = ,(a为正数).若g(7)=2.807,则g(14)= ,g(
= ,(a为正数).若g(7)=2.807,则g(14)= ,g(![]() )= .
)= .
(3)下表中与数x对应的布谷数g(x)有且仅有两个是错误的,请指出错误的布谷数,要求说明你这样找的理由,并求出正确的答案(用含a,b的代数式表示)
x |
|
| 3 | 6 | 9 | 27 |
g(x) | 1﹣4a+2b | 1﹣2a+b | 2a﹣b | 3a﹣2b | 4a﹣2b | 6a﹣3b |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知M、N直线l上两点,MN=20,O、P为线段MN上两动点,过O、P分别作长方形OABC与长方形PDEF(如图),其中,两边OA、PF分别在直线l上,图形在直线l的同侧,且OA=PF=4,CO=DP=3,动点O从点M出发,以1单位/秒的速度向右运动;同时,动点P从点N出发,以2单位/秒的速度向左运动,设运动的时间为t秒.
(1)若t=2.5秒,求点A与点F的距离;
(2)求当t为何值时,两长方形重叠部分为正方形;
(3)运动过程中,在两长方形没有重叠部分前,若能使线段AB、BC、AF的长构成三角形,求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
①4a+c<0;②m(am+b)+b>a(m≠﹣1);③关于x的一元二次方程ax2+(b﹣1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )
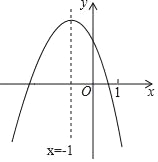
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
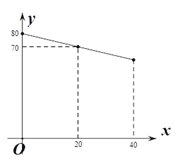
【题目】某果农的苹果园有苹果树60棵,由于提高了管理水平,可以通过补种一些苹果树的方法来提高总产量.但如果多种树,那么树之间的距离和每棵树所受的光照就会减少,单棵树的产量也随之降低.已知在一定范围内,该果园每棵果树产果y(千克)与补种果树x(棵)之间的函数关系如图所示.若超过这个范围,则会严重影响果树的产量.
(1)求y与x之间的函数关系式;
(2)在这个范围内,当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
(3)若该果农的苹果以3元/千克的价格售出,不计其他成本,按(2)的方式可以多收入多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com