
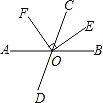
【题目】如图,直线 AB与CD相交于O,OE是∠COB的平分线,OE⊥OF.∠AOD=74°
(1)求∠BOE的度数;
(2)试说明OF平分∠AOC.
【答案】(1)37°;(2)见解析.
【解析】
(1)根据对顶角相可得∠BOC=∠AOD=74°,再根据角平分线的性质解答即可;
(2)根据邻补角的性质得∠AOC=106°,再计算出∠COF和∠AOF的度数即可.
解:(1)∵直线 AB与CD相交于O,
∴∠BOC=∠AOD=74°,
∵OE是∠COB的平分线,
∴∠BOE=∠COE=![]() ∠BOC=37°;
∠BOC=37°;
(2)∵∠AOC+∠AOD=180°,
∴∠AOC=180°﹣∠AOD=180°﹣74°=106°,
∵OE⊥OF,
∴∠EOF=90°,
∴∠COF=90°﹣∠COE=90°﹣37°=53°.
又∵∠AOF=∠AOC﹣∠COF=106°﹣53°=53°,
∴∠COF=∠AOF,
∴OF平分∠AOC.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC,连接OD,OA.
(1)求∠ODC的度数;
(2)若OB=2,OC=3,求AO的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年6月11日至17日是我国第29个全国节能宣传周,主题为“节能减耗,保卫蓝天”。某学校为配合宣传活动,抽查了某班级10天的用电量,数据如下表(单位:度):
度数 | 8 | 9 | 10 | 13 | 14 | 15 |
天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(1)这10天用电量的众数是___________,中位数是_________;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级,试估计该校6月份(30天)总的用电量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图在菱形ABCD中,AB=4,∠DAB=30°,点E是AD的中点,点M是的一个动点(不与点A重合),连接ME并廷长交CD的延长线于点N连接MD,AN.
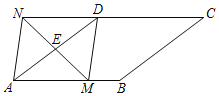
(1)求证:四边形AMDN是平行四边形;(2)当AM为何值时,四边形AMDN是矩形并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
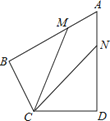
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系,△ABC的顶点均在格点上.(不写作法)
(1)以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1,并写出B1的坐标;
(2)再把△A1B1C1绕点C1 顺时针旋转90°,得到△A2B2C1,请你画出△A2B2C1,并写出B2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
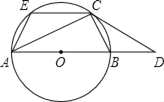
【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,过C点的切线与AB的延长线交于点D,CE∥AB交⊙O于点E,连接AC、BC、AE.
(1)求证:①∠DCB=∠CAB;②CDCE=CBCA;
(2)作CG⊥AB于点G.若tan∠CAB=![]() (k>1),求
(k>1),求![]() 的值(用含k的式子表示).
的值(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com