练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列图案中既是中心对称图形，又是轴对称图形的是（ ）

    A. B. C. D.

    【答案】C.

    【解析】试题分析：根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，以及轴对称图形的定义即可判断出．

    解：A、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项错误；

    B、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，也是轴对称图形，故此选项正确；

    C、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项错误；

    D、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项错误．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】新华文具用品店最近购进了一批钢笔，进价为每支6元，为了合理定价，在销售前4天试行机动价格，卖出时每支以10元为标准，超过10元的部分记为正，不足10元的部分记为负。文具店记录了这四天该钢笔的售价情况和售出情况，如下表所示：

    第1天

    第2天

    第3天

    第4天

    每支价格相对标准价格(元)

    +1

    0

    -1

    -2

    售出支数(支)

    12

    15

    32

    33

    (1)填空：这四天中赚钱最多的是第______天，这天赚了______元钱；

    (2)求新华文具用品店这四天出售这种钢笔一共赚了多少钱；

    (3)新华文具用品店准备用这四天赚的钱全部购进这种钢笔，进价仍为每支6元为了促销这种钢笔，每只钢笔的售价在10元的基础上打九折，本次购进的这种钢笔全部售出后共赚了多少钱?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，O为直线AB上一点，过点O作射线OC，∠AOC＝30°，将一直角三角板（∠M＝30°）的直角项点放在点O处，一边ON在射线OA上，另一边OM与OC都在直线AB的上方．

    （1）将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周．如图2，经过t秒后，ON落在OC边上，则t＝　秒（直接写结果）．

    （2）在（1）的条件下，若三角板继续转动，同时射线OC也绕O点以每秒10°的速度沿逆时针方向旋转一周，当OC转动9秒时，求∠MOC的度数．

    （3）在（2）的条件下，它们继续运动多少秒时，∠MOC＝35°？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图在中，，，是的平分线，交于点，是的中点，连接并延长交的延长线于点，连接.

    求证：（1）；

    （2）为等腰三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2﹣4ax+3a．

    （Ⅰ）求该二次函数的对称轴；

    （Ⅱ）若该二次函数的图象开口向下，当1≤x≤4时，y的最大值是2，且当1≤x≤4时，函数图象的最高点为点P，最低点为点Q，求△OPQ的面积；

    （Ⅲ）若对于该抛物线上的两点P（x1，y1），Q（x2，y2），当t≤x1≤t+1，x2≥5时，均满足y1≥y2，请结合图象，直接写出t的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O是等边三角形ABC内的一点，∠BOC＝150°，将△BOC绕点C按顺时针旋转得到△ADC，连接OD，OA．

    （1）求∠ODC的度数；

    （2）若OB＝2，OC＝3，求AO的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是小东设计的“作平行四边形ABCD，使∠B=45°，AB=2cm,BC=3cm”的作图过程．

    （1）作法：如图，①画∠B=45°；

    ②在∠B的两边上分别截取BA=2cm,BC=3cm.

    ③以点A为圆心，BC长为半径画弧，以点为圆心，AB长为半径画弧，两弧相交于点D；则四边形ABCD为所求的平行四边形．

    根据小东设计的作图过程，

    （1）使用直尺和圆规，补全图形；（保留作图痕迹）

    （2）完成下面的证明．

    证明：∵_______，_______，

    ∴四边形ABCD为所求的平行四边形．（____________）（填推理的依据）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（﹣3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H，连接BM.

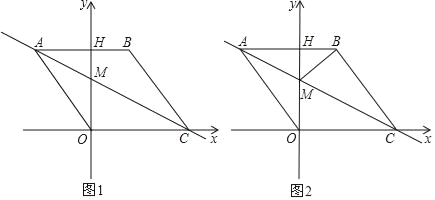
    （1）菱形ABCO的边长　 　

    （2）求直线AC的解析式；

    （3）动点P从点A出发，沿折线ABC方向以2个单位/秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒，

    ①当0＜t＜时，求S与t之间的函数关系式；

    ②在点P运动过程中，当S=3，请直接写出t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AB=AD=6，AB⊥BC，AD⊥CD，∠BAD=60°，点M、N分别在AB、AD边上，若AM：MB=AN：ND=1：2，则tan∠MCN=

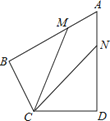
    查看答案和解析>>

    同步练习册答案