
【题目】如图,四边形ABCD是平行四边形,A, B是直线l上的两点,点B关于AD的对称点为M,连接![]() 交AD于F点.
交AD于F点.
(1)若![]() ,如图,
,如图,
①依题意补全图形;
②判断MF与FC的数量关系是 ;

(2)如图,当![]() 时,
时,![]() ,CD的延长线相交于点E,取
,CD的延长线相交于点E,取![]() E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.
E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.

【答案】(1)①见解析② FM=FC(2)CE=![]() AF
AF
【解析】
(1)①按要求画图即可;②根据“AAS”证明△AFM≌△DFC,即可证明结论成立;
(2)过点M作![]() ∥CD交AD于点G.先证明MG=AM,从而MG=CD,根据“AAS”可证△MFG≌ △CFD,进而GF=FD,HF是△CME的中位线,可得
∥CD交AD于点G.先证明MG=AM,从而MG=CD,根据“AAS”可证△MFG≌ △CFD,进而GF=FD,HF是△CME的中位线,可得![]() .再证明∠FHA=90°,根据勾股定理得出
.再证明∠FHA=90°,根据勾股定理得出![]() ,进而可求出线段CE与AF的数量关系.
,进而可求出线段CE与AF的数量关系.
(1)①如图,
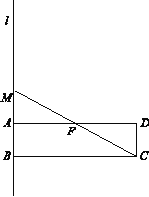
② FM=FC.
∵点B关于AD的对称点为M,
∴AB=AM.
∵四边形ABCD是平行四边形,
∴AB=CD,
∴AM=CD.
∵![]() ,
,
∴四边形ABCD是矩形,
∴∠MAF=∠CDF,
又∵∠AFM=∠CFD,
∴△AFM≌△DFC,
∴FM=FC;
(2)CE与AF的数量关系是CE=![]() AF
AF
证明:过点M作![]() ∥CD交AD于点G.
∥CD交AD于点G.
∵B,M关于AD对称,
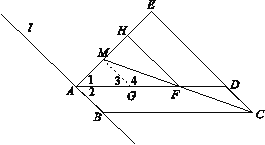
∴∠1=∠2,AB=AM.
∵四边形ABCD为平行四边形
∴AB∥CD.
∵MG∥CD,
∴MG∥AB.
∴∠2=∠3.
∴∠1=∠3.
∴AM=MG.
∵AB=AM,AB=CD,
∴MG=CD.
∵MG∥CD,
∴ ∠4=∠FDC.
∵∠MFG=∠CFD,
∴ △MFG≌ △CFD.
∴ FM=FC.
∴F为CM的中点,
∵H为ME的中点,
∴ FH∥CE,
![]()
∵∠ABC=135°, 平行四边形ABCD中,AD∥BC,
∴∠2=180°-∠ABC=45°.
∴由对称性,∠1=∠2=45°.
∵FH∥CD,AB∥CD,
∴FH∥AB.
∴∠HFA=∠2=45°.
∴∠FHA=90°,HA=HF.
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,今年2月20日举行了襄阳市首届中小学生经典诵读大赛决赛. 某中学为了选拔优秀学生参加,广泛开展校级“经典诵读”比赛活动,比赛成绩评定为A,B,C,D,E五个等级,该校七(1)班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题:
(1)该校七(1)班共有 名学生;扇形统计图中C等级所对应扇形的圆心角等于 度;
(2)补全条形统计图;
(3)若A等级的4名学生中有2名男生2名女生,现从中任意选取2名参加学校培训班,请用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.
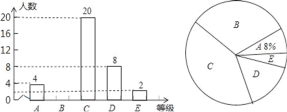
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC,连接OD,OA.
(1)求∠ODC的度数;
(2)若OB=2,OC=3,求AO的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作平行四边形ABCD,使∠B=45°,AB=2cm,BC=3cm”的作图过程.
(1)作法:如图,①画∠B=45°;

②在∠B的两边上分别截取BA=2cm,BC=3cm.
③以点A为圆心,BC长为半径画弧,以点![]() 为圆心,AB长为半径画弧,两弧相交于点D;则四边形ABCD为所求的平行四边形.
为圆心,AB长为半径画弧,两弧相交于点D;则四边形ABCD为所求的平行四边形.
根据小东设计的作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵![]() _______,
_______,![]() _______,
_______,
∴四边形ABCD为所求的平行四边形.(____________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会干部对校学生会倡导的“牵手特殊教育”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).己知A、B两组捐款人数的比为1: 5.
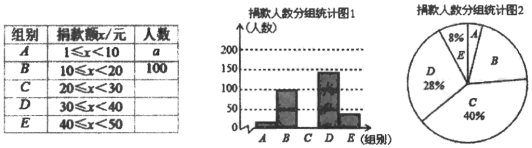
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)先求出C组的人数,再补全“捐款人数分组统计图1”
(3)根据统计情况,估计该校参加捐款的4500名学生有多少人捐款在20至40元之间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
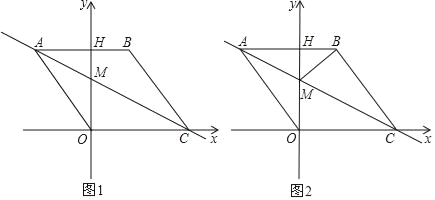
(1)菱形ABCO的边长
(2)求直线AC的解析式;
(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,
①当0<t<![]() 时,求S与t之间的函数关系式;
时,求S与t之间的函数关系式;
②在点P运动过程中,当S=3,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年6月11日至17日是我国第29个全国节能宣传周,主题为“节能减耗,保卫蓝天”。某学校为配合宣传活动,抽查了某班级10天的用电量,数据如下表(单位:度):
度数 | 8 | 9 | 10 | 13 | 14 | 15 |
天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(1)这10天用电量的众数是___________,中位数是_________;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级,试估计该校6月份(30天)总的用电量.
查看答案和解析>>
科目:初中数学 来源: 题型:
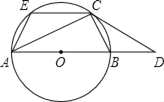
【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,过C点的切线与AB的延长线交于点D,CE∥AB交⊙O于点E,连接AC、BC、AE.
(1)求证:①∠DCB=∠CAB;②CDCE=CBCA;
(2)作CG⊥AB于点G.若tan∠CAB=![]() (k>1),求
(k>1),求![]() 的值(用含k的式子表示).
的值(用含k的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com