
【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.

(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
【答案】(1)点C的坐标为(0,3);(2)t的值为4+![]() 或4+3
或4+3![]() ;(3)t=1或4或5.6
;(3)t=1或4或5.6
【解析】试题分析:(1)由∠CBO=45°,∠BOC为直角,得到△BOC为等腰直角三角形,又OB=3,利用等腰直角三角形AOB的性质知OC=OB=3,然后由点C在y轴的正半轴可以确定点C的坐标;
(2)需要对点P的位置进行分类讨论:①当点P在点B右侧时,如图2所示,由∠BCO=45°,用∠BCO-∠BCP求出∠PCO为30°,又OC=3,在Rt△POC中,利用锐角三角函数定义及特殊角的三角函数值求出OP的长,由PQ=OQ+OP求出运动的总路程,由速度为1个单位/秒,即可求出此时的时间t;②当点P在点B左侧时,如图3所示,用∠BCO+∠BCP求出∠PCO为60°,又OC=3,在Rt△POC中,利用锐角三角函数定义及特殊角的三角函数值求出OP的长,由PQ=OQ+OP求出运动的总路程,由速度为1个单位/秒,即可求出此时的时间t;
(3)当⊙P与四边形ABCD的边(或边所在的直线)相切时,分三种情况考虑:
①当⊙P与BC边相切时,利用切线的性质得到BC垂直于CP,可得出∠BCP=90°,由∠BCO=45°,得到∠OCP=45°,即此时△COP为等腰直角三角形,可得出OP=OC,由OC=3,得到OP=3,用OQ-OP求出P运动的路程,即可得出此时的时间t;
②当⊙P与CD相切于点C时,P与O重合,可得出P运动的路程为OQ的长,求出此时的时间t;
③当⊙P与AD相切时,利用切线的性质得到∠DAO=90°,得到此时A为切点,由PC=PA,且PA=9-t,PO=t-4,在Rt△OCP中,利用勾股定理列出关于t的方程,求出方程的解得到此时的时间t.
综上,得到所有满足题意的时间t的值.
试题解析::(1)∵∠BCO=∠CBO=45°,
∴OC=OB=3,
又∵点C在y轴的正半轴上,
∴点C的坐标为(0,3);
(2)分两种情况考虑:
①当点P在点B右侧时,如图2,
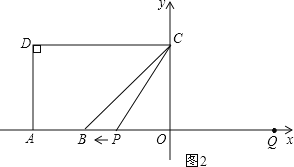
若∠BCP=15°,得∠PCO=30°,
故PO=COtan30°=![]() ,此时t=4+
,此时t=4+![]() ;
;
②当点P在点B左侧时,如图3,
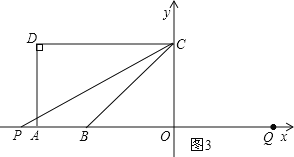
由∠BCP=15°,得∠PCO=60°,
故OP=COtan60°=3![]() ,
,
此时,t=4+3![]() ,
,
∴t的值为4+![]() 或4+3
或4+3![]() ;
;
(3)由题意知,若⊙P与四边形ABCD的边相切时,有以下三种情况:
①当⊙P与BC相切于点C时,有∠BCP=90°,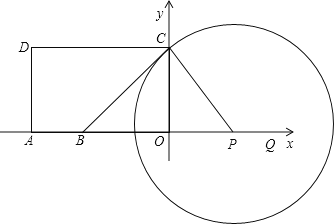
从而∠OCP=45°,得到OP=3,此时t=1;
②当⊙P与CD相切于点C时,有PC⊥CD,即点P与点O重合,此时t=4;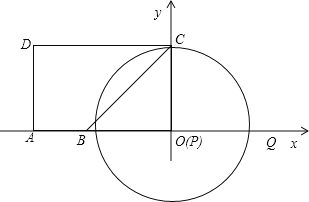
③当⊙P与AD相切时,由题意,得∠DAO=90°,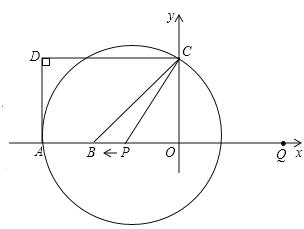
∴点A为切点,如图4,PC2=PA2=(9-t)2,PO2=(t-4)2,
于是(9t)2=(t-4)2+32,即81-18t+t2=t2-8t+16+9,
解得:t=5.6,
∴t的值为1或4或5.6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC,连接OD,OA.
(1)求∠ODC的度数;
(2)若OB=2,OC=3,求AO的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会干部对校学生会倡导的“牵手特殊教育”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).己知A、B两组捐款人数的比为1: 5.
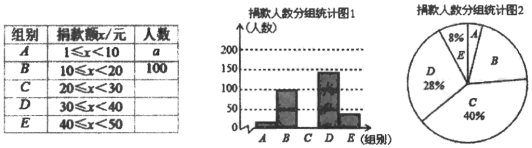
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)先求出C组的人数,再补全“捐款人数分组统计图1”
(3)根据统计情况,估计该校参加捐款的4500名学生有多少人捐款在20至40元之间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
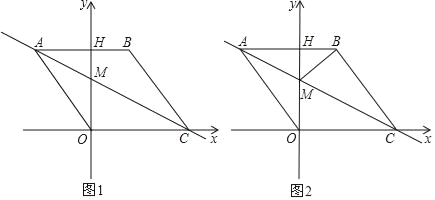
(1)菱形ABCO的边长
(2)求直线AC的解析式;
(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,
①当0<t<![]() 时,求S与t之间的函数关系式;
时,求S与t之间的函数关系式;
②在点P运动过程中,当S=3,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD交于点F,AC⊥AB于点A,点E在边CD上,且满足DFDB=DEDC,FE=FB,BD平分∠ABE,若AB=6,CF=9,则OE的长为_____.
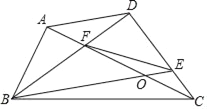
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年6月11日至17日是我国第29个全国节能宣传周,主题为“节能减耗,保卫蓝天”。某学校为配合宣传活动,抽查了某班级10天的用电量,数据如下表(单位:度):
度数 | 8 | 9 | 10 | 13 | 14 | 15 |
天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(1)这10天用电量的众数是___________,中位数是_________;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级,试估计该校6月份(30天)总的用电量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图在菱形ABCD中,AB=4,∠DAB=30°,点E是AD的中点,点M是的一个动点(不与点A重合),连接ME并廷长交CD的延长线于点N连接MD,AN.
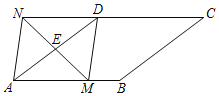
(1)求证:四边形AMDN是平行四边形;(2)当AM为何值时,四边形AMDN是矩形并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com