
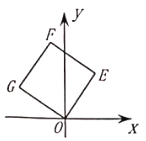
【题目】如图,将正方形![]() 放在平面直角坐标系中,
放在平面直角坐标系中,![]() 是坐标原点,点
是坐标原点,点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为__________.
的坐标为__________.
【答案】![]()
【解析】
过点E作EI⊥x轴于I,过点G作GH⊥x轴于H,根据同角的余角相等求出∠OEI=∠GOH,再利用“角角边”证明△EOI和△OGH全等,根据全等三角形对应边相等可得OH=EI,EI=OI,然后根据点G在第二象限写出坐标即可.
解:过点E作EI⊥x轴于I,过点G作GH⊥x轴于H,如图所示:

∵四边形OEFG是正方形,
∴OE=OG,∠EOG =90°,
∴∠GOH+∠EOI=90°,
又∵∠OEI +∠EOI=90°,
∴∠OEI =∠GOH,
在△EOI和△OGH中, ,
,
∴△EOI≌△OGH(AAS),
∴OH=EI=3,GH=OI=2,
∵点G在第二象限,
∴点G的坐标为(-3,2).
故答案为(-3,2).


科目:初中数学 来源: 题型:
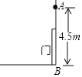
【题目】如图,有一个由传感器A控制的灯,要装在门上方离地面4.5m的墙上,任何东西只要移至该灯5m及5m内,灯就会自动发光,小明身高1.5m,他走到离墙_______的地方灯刚好发光.
查看答案和解析>>
科目:初中数学 来源: 题型:
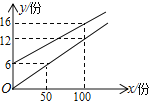
【题目】武汉市某校实行学案式教学,需印制若干份数学学案.印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示
(1) 求甲、乙两种收费方式的函数关系式;
(2) 当印刷多少份学案时,两种印刷方式收费一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华文具用品店最近购进了一批钢笔,进价为每支6元,为了合理定价,在销售前4天试行机动价格,卖出时每支以10元为标准,超过10元的部分记为正,不足10元的部分记为负。文具店记录了这四天该钢笔的售价情况和售出情况,如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
每支价格相对标准价格(元) | +1 | 0 | -1 | -2 |
售出支数(支) | 12 | 15 | 32 | 33 |
(1)填空:这四天中赚钱最多的是第______天,这天赚了______元钱;
(2)求新华文具用品店这四天出售这种钢笔一共赚了多少钱;
(3)新华文具用品店准备用这四天赚的钱全部购进这种钢笔,进价仍为每支6元为了促销这种钢笔,每只钢笔的售价在10元的基础上打九折,本次购进的这种钢笔全部售出后共赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
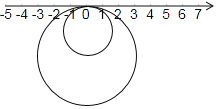
【题目】如图,半径为1的小圆与半径为2的大圆上有一点与数轴上原点重合,两圆在数轴上做无滑动的滚动,小圆的运动速度为每秒π个单位,大圆的运动速度为每秒2π个单位.
(1)若大圆沿数轴向左滚动1周,则该圆与数轴重合的点所表示的数是 ;
(2)若小圆不动,大圆沿数轴来回滚动,规定大圆向右滚动时间记为正数,向左滚动时间记为负数,依次滚动的情况记录如下(单位:秒):﹣1,+2,﹣4,﹣2,+3,﹣8
①第几次滚动后,大圆离原点最远?
②当大圆结束运动时,大圆运动的路程共有多少?此时两圆与数轴重合的点之间的距离是多少?(结果保留π)
(3)若两圆同时在数轴上各自沿着某一方向连续滚动,滚动一段时间后两圆与数轴重合的点之间相距9π,求此时两圆与数轴重合的点所表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,今年2月20日举行了襄阳市首届中小学生经典诵读大赛决赛. 某中学为了选拔优秀学生参加,广泛开展校级“经典诵读”比赛活动,比赛成绩评定为A,B,C,D,E五个等级,该校七(1)班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题:
(1)该校七(1)班共有 名学生;扇形统计图中C等级所对应扇形的圆心角等于 度;
(2)补全条形统计图;
(3)若A等级的4名学生中有2名男生2名女生,现从中任意选取2名参加学校培训班,请用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.
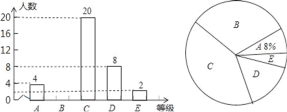
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 是正方形内两点,
是正方形内两点,![]() ,
,![]() ,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程:
,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程:
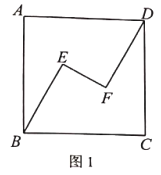
(1)在图1中,连接![]() ,且
,且![]()
①求证:![]() 与
与![]() 互相平分;
互相平分;
②求证:![]() ;
;
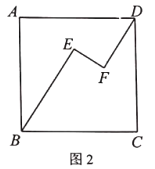
(2)在图2中,当![]() ,其它条件不变时,
,其它条件不变时,![]() 是否成立?若成立,请证明:若不成立,请说明理由.
是否成立?若成立,请证明:若不成立,请说明理由.
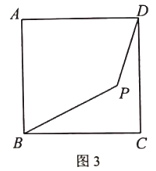
(3)在图3中,当![]() ,
,![]() ,
,![]() 时,求
时,求![]() 之长.
之长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角项点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.

(1)将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周.如图2,经过t秒后,ON落在OC边上,则t= 秒(直接写结果).
(2)在(1)的条件下,若三角板继续转动,同时射线OC也绕O点以每秒10°的速度沿逆时针方向旋转一周,当OC转动9秒时,求∠MOC的度数.
(3)在(2)的条件下,它们继续运动多少秒时,∠MOC=35°?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作平行四边形ABCD,使∠B=45°,AB=2cm,BC=3cm”的作图过程.
(1)作法:如图,①画∠B=45°;

②在∠B的两边上分别截取BA=2cm,BC=3cm.
③以点A为圆心,BC长为半径画弧,以点![]() 为圆心,AB长为半径画弧,两弧相交于点D;则四边形ABCD为所求的平行四边形.
为圆心,AB长为半径画弧,两弧相交于点D;则四边形ABCD为所求的平行四边形.
根据小东设计的作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵![]() _______,
_______,![]() _______,
_______,
∴四边形ABCD为所求的平行四边形.(____________)(填推理的依据).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com