
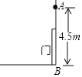
【题目】如图,有一个由传感器A控制的灯,要装在门上方离地面4.5m的墙上,任何东西只要移至该灯5m及5m内,灯就会自动发光,小明身高1.5m,他走到离墙_______的地方灯刚好发光.
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=6,AD⊥BC于点D.点P在边AB上运动,过点P作PE∥BC,与边AC交于点E,连接ED,以PE、ED为邻边作平行四边形PEDF.设线段AP的长为x(0<x<6). 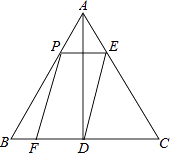
(1)求线段PE的长.(用含x的代数式表示)
(2)当四边形PEDF为菱形时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
(1)在图中作出![]() 关于
关于![]() 轴对称的
轴对称的![]() .
.
(2)写出点![]() 的坐标(直接写答案).
的坐标(直接写答案).
A1_____________,B1______________,C1______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )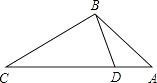
A.∠ABD=∠C
B.∠ADB=∠ABC
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
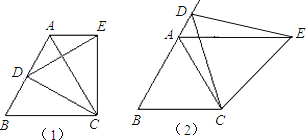
【题目】(如图1,等边△ABC中,D是AB边上的点,以CD为一边,向上作等边△EDC,连接AE.
(1)求证:△DBC≌△EAC;
(2)求证:AE∥BC;
(3)如图2, 若D在边BA的延长线上,且AB=6,AD=2,试求△ABC与△EAC面积的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.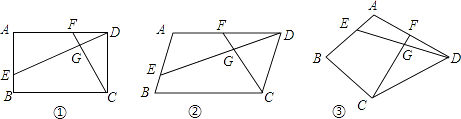
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证:△ADE∽△DCF;
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时, ![]() 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图③,若BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF,请直接写出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣3,﹣1,0,1,3这五个数中随机抽取一个数记为a,再从剩下的四个数中任意抽取一个数记为b,恰好使关于x,y的二元一次方程组 ![]() 有整数解,且点(a,b)落在双曲线
有整数解,且点(a,b)落在双曲线 ![]() 上的概率是 .
上的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,△ABC是直角三角形,∠ACB=90°,点B、C都在第一象限内,CA⊥x轴,垂足为点A,反比例函数y1= ![]() 的图象经过点B;反比例函数y2=
的图象经过点B;反比例函数y2= ![]() 的图象经过点C(
的图象经过点C( ![]() ,m).
,m).
(1)求点B的坐标;
(2)△ABC的内切圆⊙M与BC,CA,AB分别相切于D,E,F,求圆心M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com