
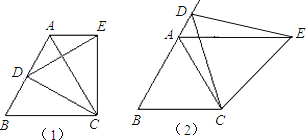
【题目】(如图1,等边△ABC中,D是AB边上的点,以CD为一边,向上作等边△EDC,连接AE.
(1)求证:△DBC≌△EAC;
(2)求证:AE∥BC;
(3)如图2, 若D在边BA的延长线上,且AB=6,AD=2,试求△ABC与△EAC面积的比值.
【答案】(1)详见解析,(2)详见解析,(3)![]() .
.
【解析】
(1)已知的条件有AC=BC,CE=CD,我们发现∠BCD和∠ACE都是60°减去一个∠ACD,因此两三角形全等的条件就都凑齐了(SAS);
(2)要证AE∥BC,关键是证∠EAC=∠ACB,由于∠ACB=∠ACB,那么关键是证∠EAC=∠ACB,根据(1)的全等三角形,我们不难得出这两个角相等,也就得出了证平行的条件.
(3)同(1)(2)的思路完全相同,也是通过先证明△BCD和△ACE全等,即可得到△ABC与△EAC面积的比值.
(1)证明:∵∠ACB=60°,∠DCE=60°,
∴∠BCD=60°∠ACD,∠ACE=60°∠ACD,
∴∠BCD=∠ACE,
在△DBC和△EAC中,
∵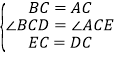 ,
,
∴△DBC≌△EAC(SAS),
(2)∵△DBC≌△EAC,
∴∠EAC=∠B=60°,
又∠ACB=60°,
∴∠EAC=∠ACB,
∴AE∥BC;
(3)结论:AE∥BC,
理由:∵△ABC、△EDC为等边三角形,
∴BC=AC,DC=CE,∠BCA=∠DCE=60°,
∠BCA+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE,
在△DBC和△EAC中,
∵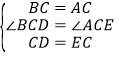 ,
,
∴△DBC≌△EAC(SAS),
∴∠EAC=∠B=60°,AE=BD
又∠ACB=60°,
∴∠EAC=∠ACB,
∴AE∥BC;
设AE,BC两平行线间的距离为h
∵AB=6,AD=2,
∴S△ABC=![]() BCh=
BCh=![]() ×6h=3h,
×6h=3h,
S△ACE=![]() AEh=
AEh=![]() ×8h=4h
×8h=4h
∴S△ABC∶S△AEC=![]()
则△ABC与△EAC面积的比值为![]() .
.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】定义:我们把平面内与一个定点F和一条定直线l(l不经过点F)距离相等的点的轨迹(满足条件的所有点所组成的图形)叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.
(1)已知抛物线的焦点F(0, ![]() ),准线l:
),准线l: ![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)已知抛物线的解析式为:y=x2﹣n2 , 点A(0, ![]() )(n≠0),B(1,2﹣n2),P为抛物线上一点,求PA+PB的最小值及此时P点坐标;
)(n≠0),B(1,2﹣n2),P为抛物线上一点,求PA+PB的最小值及此时P点坐标;
(3)若(2)中抛物线的顶点为C,抛物线与x轴的两个交点分别是D、E,过C、D、E三点作⊙M,⊙M上是否存在定点N?若存在,求出N点坐标并指出这样的定点N有几个;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
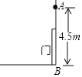
【题目】如图,有一个由传感器A控制的灯,要装在门上方离地面4.5m的墙上,任何东西只要移至该灯5m及5m内,灯就会自动发光,小明身高1.5m,他走到离墙_______的地方灯刚好发光.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波火车站北广场将于2015年底投入使用,计划在广场内种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y=![]() 交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的面积是__.
交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的面积是__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com