
����Ŀ��ij��˾������һ���µĽ��ܲ�Ʒ���ò�Ʒ�ijɱ���Ϊ6Ԫ/�����ò�Ʒ����ʽͶ���г�ǰͨ�������������Ϊ��һ����(30��)�������ۣ��ۼ�Ϊ10Ԫ/����������Ա��������������˸��ټ�¼��������¼������Ƴ�ͼ��ͼ�е�����ABC��ʾ��������y(��)������ʱ��x(��)֮��ĺ�����ϵ��

(1)��y��x֮��ĺ�������ʽ����д��x��ȡֵ��Χ��
(2)���ý��ܲ�Ʒ������������ΪW(Ԫ)����W��x֮��ĺ�������ʽ�������������������1040Ԫ���������ж����죿
(3)��5��x��17��ֱ��д���ڼ�������������������������������Ƕ���Ԫ��
���𰸡���1��![]() ����2��������������1040Ԫ����������18������3����5�������������������������������880Ԫ.
����2��������������1040Ԫ����������18������3����5�������������������������������880Ԫ.
��������
��1������һ���ֶκ��������ô���ϵ������y��x֮��ĺ�������ʽ����ȷ��x��ȡֵ��Χ��
��2����������=���ۼ�-�ɱ��������������ɵ�w��x֮��ĺ�������ʽ�����ֱ���ݷֶκ�������������������1040Ԫ��Ӧ��x��ֵ��
��3���ֱ����5��x��10��10<x��17������Χ��������������Աȿɵý��ۣ�
��1�����߶�AB������ʾ�ĺ�����ϵʽΪy=ax+b��1��x��10����
BC�α�ʾ�ĺ�����ϵʽΪy=mx+n��10��x��30����
�ѣ�1,300������10,120������y=ax+b�е�![]() �����
�����![]() ��
��
���߶�AB��ʾ�ĺ�����ϵʽΪy=-20x+320��1��x��10����
�ѣ�10,120������30,400������y=mx+n�е�![]() �����
�����![]() ��
��
���߶�BC��ʾ�ĺ�����ϵʽΪy=14x-20��10��x��30����
��������![]() .
.
��2���������֪������Ʒ������Ϊ10-6=4(Ԫ/��)��
�൱1��x��10ʱ��w=4����-20x+320��=-80x+1280��
��10��x��30ʱ��w=4����14x-20��=56x-80��
��![]() ,������������1040Ԫ����w��1040��
,������������1040Ԫ����w��1040��
�൱1��x��10ʱ��w=-80x+1280��1040�����x��3��
��10��x��30ʱ��w=56x-80��1040�����x��20��
��3��x��20����������������1040Ԫ����������18��.
��3����5��x��17����5�������������������������������880Ԫ.


 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����DΪBC��һ�㣬��ADΪ����������ADE��AD=AE����BAC=��DAE������CE��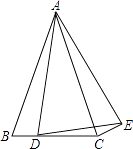
��1����֤��BD=CE��
��2����֪BC=8����BAC=��DAE=30�㣬����DCE�����Ϊ1�����߶�BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
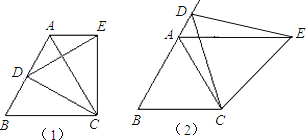
����Ŀ��(��ͼ1���ȱߡ�ABC�У�D��AB���ϵĵ㣬��CDΪһ�ߣ��������ȱߡ�EDC������AE��
��1����֤:��DBC�ա�EAC��
��2����֤:AE��BC��
��3����ͼ2, ��D�ڱ�BA���ӳ�����,��AB=6,AD=2,�����ABC���EAC����ı�ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=x2����m+3��x+9�Ķ���C��x���������ϣ�һ�κ���y=x+3�������߽���A��B���㣬��x��y��ֱ���D��E���㣮
��1����m��ֵ��
��2����A��B��������ꣻ
��3������3��x��1ʱ�������������Ƿ����һ��P��ʹ�á�PAB������ǡ�ABC�����2���������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ө�3����1��0��1��3��������������ȡһ������Ϊa���ٴ�ʣ�µ��ĸ����������ȡһ������Ϊb��ǡ��ʹ����x��y�Ķ�Ԫһ�η����� ![]() �������⣬�ҵ㣨a��b������˫����
�������⣬�ҵ㣨a��b������˫���� ![]() �ϵĸ����� ��
�ϵĸ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڼ䣬һЩͬѧ��Ҫ��A��B��C��D�ĸ��ط��μӶ���Ӫ����ִ���Щͬѧ�����������һ����ͬѧ�����ݵ����������Ƴ�����������ͳ��ͼ�� 
��1������A��Բ�ĽǵĶ���Ϊ �� ���˴ζ���Ӫһ����320��ѧ���μӣ���ǰ��C�ص�ѧ��Լ���ˣ���������ͳ��ͼ����������
��2����ij���������ֻ����һ�˲μӣ������������һ����Ϸ��ȷ���μ��ߣ���4����״����С��ȫ��ͬ�Ŀ�Ƭ�Ϸֱ�д�ϩ�1��1��2��3�ĸ����������ý������س�ȡһ�ţ����ɵܴܵ����µ����ſ�Ƭ������س�ȡһ�ţ�����ȡ�����ſ�Ƭ�ϵ�����֮��С��3����μӣ�����ܵܲμӣ����б�������״ͼ�������ַ����Խ�����Ƿ�ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�͡�DEC���ǵ���ֱ�������Σ�CΪ���ǵĹ���ֱ�Ƕ��㣬��AD��BE��FΪ�߶�AD���е㣬����CF
��1����ͼ1����D����BC��ʱ����֤����BE=2CF����BE��CF��
��2����ͼ2���ѡ�DEC��C��˳ʱ����תһ����ǣ������������䣬�ʣ�1���еĹ�ϵ�Ƿ���Ȼ���������������֤�����������������д����Ӧ����ȷ�Ľ��۲�����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪AE��AB��AF��AC��AE=AB��AF=AC.��֤����1��EC=BF����2��EC��BF.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ�����������ĸ����ۣ���abc=0����a+b+c��0����a��b����4ac��b2��0��������ȷ������ �� 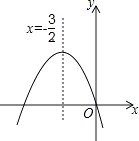
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com