
【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:(1)EC=BF;(2)EC⊥BF.

【答案】见解析
【解析】
试题(1)先求出∠EAC=∠BAF,然后利用“边角边”证明△ABF和△AEC全等,根据全等三角形对应边相等即可证明;
(2)根据全等三角形对应角相等可得∠AEC=∠ABF,设AB、CE相交于点D,根据∠AEC+∠ADE=90°可得∠ABF+∠ADM=90°,再根据三角形内角和定理推出∠BMD=90°,从而得证.
证明:(1)∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°,
∴∠BAE+∠BAC=∠CAF+∠BAC,
即∠EAC=∠BAF,
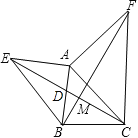
在△ABF和△AEC中,
∵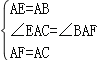 ,
,
∴△ABF≌△AEC(SAS),
∴EC=BF;
(2)如图,根据(1),△ABF≌△AEC,
∴∠AEC=∠ABF,
∵AE⊥AB,
∴∠BAE=90°,
∴∠AEC+∠ADE=90°,
∵∠ADE=∠BDM(对顶角相等),
∴∠ABF+∠BDM=90°,
在△BDM中,∠BMD=180°﹣∠ABF﹣∠BDM=180°﹣90°=90°,
所以EC⊥BF.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是半圆,连接AB,点O为AB的中点,点C,D在
是半圆,连接AB,点O为AB的中点,点C,D在 ![]() 上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( ) 
A.26°
B.28°
C.30°
D.32°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在新晚报举办的“万人户外徒步活动”中,为统计参加活动人员的年龄情况,从参加人员中随机抽取了若干人的年龄作为样本,进行数据统计,制成如图的条形统计图和扇形统计图(部分). 
(1)本次活动统计的样本容量是多少?
(2)求本次活动中70岁以上的人数,并补全条形统计图;
(3)本次参加活动的总人数约为12000人,请你估算参加活动人数最多的年龄段的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y=![]() 交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的面积是__.
交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的面积是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为:A(﹣2,3)、B(﹣6,0)、C(﹣1,0). 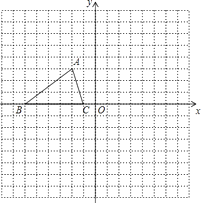
(1)将△ABC沿y轴翻折,画出翻折后的△A1B1C1 , 点A的对应点A1的坐标是
(2)△ABC关于x轴对称的图形△A2B2C2 , 直接写出点A2的坐标
(3)若△DBC与△ABC全等(点D与点A重合除外),请直接写出满足条件点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com