
【题目】如图,△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,连AD,BE,F为线段AD的中点,连接CF
(1)如图1,当D点在BC上时,求证:①BE=2CF,②BE⊥CF.
(2)如图2,把△DEC绕C点顺时针旋转一个锐角,其他条件不变,问(1)中的关系是否仍然成立?如果成立请证明.如果不成立,请写出相应的正确的结论并加以证明.
【答案】
(1)
证明:
①∵△ABC和△DEC都是等腰直角三角形,
∴BC=AC,CD=CE,∠ACB=∠ECD=90°,
在△BCE和△ACD中
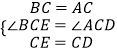
∴△BCE≌△ACD(SAS),
∴BE=AD,∠EBC=∠DAC,
∵F为线段AD的中点,
∴CF=AF=DF= ![]() AD
AD
∴BE=2CF;
②∵AF=CF,
∴∠DAC=∠FCA,
∵∠BCF+∠ACF=90°,
∴∠BCF+∠EBC=90°,
即BE⊥CF;
(2)
证明:旋转一个锐角后,(1)中的关系依然成立.
证明:如图2,延长CF到M,使FM=FC,连接AM,DM,
又AF=DF,
∴四边形AMDC为平行四边形
∴AM=CD=CE,∠MAC=180°﹣∠ACD,
∠BCE=∠BCA+∠DCE﹣∠ACD=180°﹣∠ACD,
即∠MAC=∠BCE,
在△MAC和△ECB中
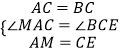
∴△MAC≌△ECB(SAS),
∴CM=BE;∠ACM=∠CBE,
∴BE=CM=2CF;
∴∠CBE+∠BCM=∠ACM+∠BCM=90°,
即BE⊥CF.
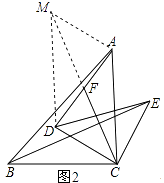
【解析】(1)①由条件可证明Rt△ADC≌Rt△BEC,可证得BE=AD,再利用直角三角形的性质可证明BE=2CF;②由直角三角形的性质可得CF=DF,可证明∠FCD=∠ADC,可证得∠EBC+∠FCD=90°,可证明结论;(2)延长CF到M,使FM=FC,连接AM,DM,可证明四边形ACDM为平行四边形,进一步可证明△MAC≌△ECB,则可得MC=BE,可证得BE=2CF,再结合∠ACB=90°,可证明BE⊥CF.
【考点精析】利用等腰直角三角形对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波火车站北广场将于2015年底投入使用,计划在广场内种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
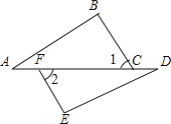
【题目】如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的有_____.
①∠E=∠B;②ED=BC;③AB=EF;④AF=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是半圆,连接AB,点O为AB的中点,点C,D在
是半圆,连接AB,点O为AB的中点,点C,D在 ![]() 上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( ) 
A.26°
B.28°
C.30°
D.32°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y=![]() 交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的面积是__.
交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的面积是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A( ![]() ,0),点B(0,1),点0(0,0).过边OA上的动点M(点M不与点O,A重合)作MN丄AB于点N,沿着MN折叠该纸片,得顶点A的对应点A′,设OM=m,折叠后的△AM′N与四边形OMNB重叠部分的面积为S.
,0),点B(0,1),点0(0,0).过边OA上的动点M(点M不与点O,A重合)作MN丄AB于点N,沿着MN折叠该纸片,得顶点A的对应点A′,设OM=m,折叠后的△AM′N与四边形OMNB重叠部分的面积为S.
(1)如图①,当点A′与顶点B重合时,求点M的坐标;
(2)如图②,当点A′,落在第二象限时,A′M与OB相交于点C,试用含m的式子表示S;
(3)当S= ![]() 时,求点M的坐标(直接写出结果即可).
时,求点M的坐标(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com