
【题目】如图,在△ABC中,AB=AC,点D为BC上一点,以AD为腰作等腰△ADE,AD=AE,∠BAC=∠DAE,连接CE.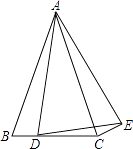
(1)求证:BD=CE;
(2)已知BC=8,∠BAC=∠DAE=30°,若△DCE的面积为1,求线段BD的长.
【答案】
(1)
证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠EAC,
在△ABD和△ACE中,
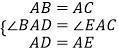 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)
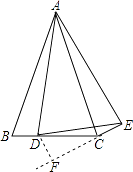
解: 过D作DF⊥EC交EC的延长线于F,
∵△ABD≌△ACE,
∴∠ACE=∠B,
∵∠BAC=30°,
∴∠B+∠ACB=150°,
∴∠BCE=∠ACB+∠ACE=150°,
∴∠DCF=30°,
∴DF= ![]() CD=
CD= ![]() (BC﹣BD)=
(BC﹣BD)= ![]() (8﹣BD),
(8﹣BD),
∵CE=BD,
∴DF=4﹣ ![]() CE,
CE,
∵△DCE的面积为1,
∴ ![]() DFCE=
DFCE= ![]() CFBD=
CFBD= ![]() (8﹣BD)BD=1,
(8﹣BD)BD=1,
解得:BD=4﹣ ![]() ,BD=4+
,BD=4+ ![]() (不合题意,舍去).
(不合题意,舍去).
【解析】(1)易证∠BAD=∠EAC,即可证明△ABD≌△ACE,即可得到结论;(2)过D作DF⊥EC交EC的延长线于F,由△ABD≌△ACE,得到∠ACE=∠B,根据∠BAC=30°,于是得到∠B+∠ACB=150°,等量代换得到∠BCE=∠ACB+∠ACE=150°,由邻补角的性质得到∠DCF=30°,根据直角三角形的性质得到DF= ![]() CD=
CD= ![]() (BC﹣BD)=
(BC﹣BD)= ![]() (8﹣BD),根据△DCE的面积为1,列方程即可得到结论.
(8﹣BD),根据△DCE的面积为1,列方程即可得到结论.
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等.


科目:初中数学 来源: 题型:
【题目】定义:我们把平面内与一个定点F和一条定直线l(l不经过点F)距离相等的点的轨迹(满足条件的所有点所组成的图形)叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.
(1)已知抛物线的焦点F(0, ![]() ),准线l:
),准线l: ![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)已知抛物线的解析式为:y=x2﹣n2 , 点A(0, ![]() )(n≠0),B(1,2﹣n2),P为抛物线上一点,求PA+PB的最小值及此时P点坐标;
)(n≠0),B(1,2﹣n2),P为抛物线上一点,求PA+PB的最小值及此时P点坐标;
(3)若(2)中抛物线的顶点为C,抛物线与x轴的两个交点分别是D、E,过C、D、E三点作⊙M,⊙M上是否存在定点N?若存在,求出N点坐标并指出这样的定点N有几个;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
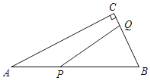
【题目】已知,如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=18cm.动点P从点A出发,沿AB向点B运动,动点Q从点B出发,沿BC向点C运动,如果动点P以2cm/s,Q以1cm/s的速度同时出发,设运动时间为t(s),解答下列问题:
(1)t为何值时,△PBQ是等边三角形?
(2)P,Q在运动过程中,△PBQ的形状不断发生变化,当t为何值时,△PBQ是直角三角形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
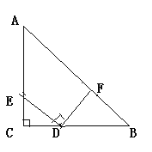
【题目】如图,已知∠ACB=90°,AC=BC,BD⊥DE,AE⊥DE,垂足分别为D、E.(这几何模型具备“一线三直角”)如下图:
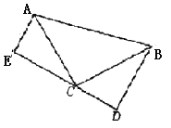
(1)①请你证明:△ACE≌△CBD;②若AE=3,BD=5,求DE的长;
(2)迁移:如图:在等腰Rt△ABC中,且∠C=90°,CD=2,BD=3,D、E分别是边BC,AC上的点,将DE绕点D顺时针旋转90°,点E刚好落在边AB上的点F处,则CE=________。(不要求写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com