
【题目】寒假期间,一些同学将要到A,B,C,D四个地方参加冬令营活动,现从这些同学中随机调查了一部分同学.根据调查结果,绘制成了如下两幅统计图: 
(1)扇形A的圆心角的度数为 , 若此次冬令营一共有320名学生参加,则前往C地的学生约有人,并将条形统计图补充完整;
(2)若某姐弟两人中只能有一人参加,姐弟俩决定用一个游戏来确定参加者:在4张形状、大小完全相同的卡片上分别写上﹣1,1,2,3四个整数,先让姐姐随机地抽取一张,再由弟弟从余下的三张卡片中随机地抽取一张.若抽取的两张卡片上的数字之和小于3则姐姐参加,否则弟弟参加.用列表法或树状图分析这种方法对姐弟俩是否公平?
【答案】
(1)108;64
(2)解:根据题意列表如下:
﹣1 | 1 | 2 | 3 | |
﹣1 | ﹣﹣﹣ | (1,﹣1) | (2,﹣1) | (3,﹣1) |
1 | (﹣1,1) | ﹣﹣﹣ | (2,1) | (3,1) |
2 | (﹣1,2) | (1,2) | ﹣﹣﹣ | (3,2) |
3 | (﹣1,3) | (1,3) | (2,3) | ﹣﹣﹣ |
所有等可能的情况有12种,其中抽取的两张卡片上的数字之和小于3的情况有6种,
∴P(数字之和小于3)=P(数字之和大于等于3)= ![]() =
= ![]() ,
,
则此游戏公平.
【解析】解:(1)由题意得:(30+20+10)÷(1﹣40%)=100(人),
则扇形A的圆心角的度数为 ![]() ×360°=108°;
×360°=108°;
此次冬令营一共有320名学生参加,则前往C地的学生约有: ![]() ×320=64(人);
×320=64(人);
B营地的人数是:100×40%=40(人),
补全条形统计图,如图所示;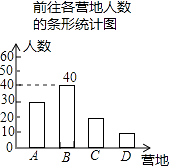
所以答案是:108;64;
【考点精析】认真审题,首先需要了解扇形统计图(能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况),还要掌握条形统计图(能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况)的相关知识才是答题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D在同一条直线上,点E、F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
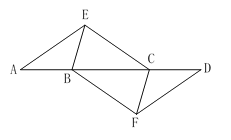
(1)求证:△ACE≌△DBF;
(2)求证:四边形BFCE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
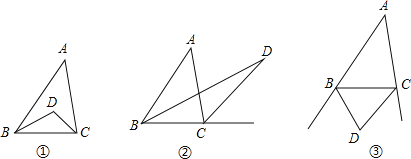
【题目】如图①,△ABC中,DC,BD分别是∠ACB和∠ABC的平分线,且∠A=α
(1)用含α的代数式表示∠CDB;
(2)若把图①中∠ACB的平分线DC改为∠ACB的外角的平分线(如图②),怎样用含α的代数式表示∠CDB.
(3)若把图①中“DC,DB分别是∠ACB和∠ABC的平分线”改成“DC,BD分别是∠ACB和∠ABC的外角的平分线”,(如图③),怎样用含α的代数式表示∠CDB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是半圆,连接AB,点O为AB的中点,点C,D在
是半圆,连接AB,点O为AB的中点,点C,D在 ![]() 上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( ) 
A.26°
B.28°
C.30°
D.32°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在新晚报举办的“万人户外徒步活动”中,为统计参加活动人员的年龄情况,从参加人员中随机抽取了若干人的年龄作为样本,进行数据统计,制成如图的条形统计图和扇形统计图(部分). 
(1)本次活动统计的样本容量是多少?
(2)求本次活动中70岁以上的人数,并补全条形统计图;
(3)本次参加活动的总人数约为12000人,请你估算参加活动人数最多的年龄段的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.
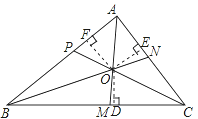
已知:如图,AM,BN,CP是△ABC的三条角平分线.
求证:AM、BN、CP交于一点.
证明:如图,设AM,BN交于点O,过点O分别作OD⊥BC,OF⊥AB,垂足分别为点D,E,F.
∵O是∠BAC角平分线AM上的一点( ),
∴OE=OF( ).
同理,OD=OF.
∴OD=OE( ).
∵CP是∠ACB的平分线( ),
∴O在CP上( ).
因此,AM,BN,CP交于一点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com