
【题目】阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.
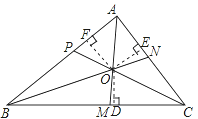
已知:如图,AM,BN,CP是△ABC的三条角平分线.
求证:AM、BN、CP交于一点.
证明:如图,设AM,BN交于点O,过点O分别作OD⊥BC,OF⊥AB,垂足分别为点D,E,F.
∵O是∠BAC角平分线AM上的一点( ),
∴OE=OF( ).
同理,OD=OF.
∴OD=OE( ).
∵CP是∠ACB的平分线( ),
∴O在CP上( ).
因此,AM,BN,CP交于一点.
【答案】已知;角平分线上的一点到这个角的两边的距离相等;等量代换;已知;角的内部到角的两边距离相等的点在这个角的平分线上.
【解析】
此题先利用角平分线性质得到O到各边的距离相等,再利用角平分线性质定理逆定理,得到O在第三个角的平分线上,从而证明结论成立.
证明:设AM,BN交于点O,过点O分别作OD⊥BC,OF⊥AB,垂足分别为点D,E,F.
∵O是∠BAC角平分线AM上的一点(已知),
∴OE=OF(角平分线上的一点到这个角的两边的距离相等).
同理,OD=OF.
∴OD=OE(等量代换).
∵CP是∠ACB的平分线(已知),
∴O在CP上(角的内部到角的两边距离相等的点在这个角的平分线上).
因此,AM,BN,CP交于一点.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】寒假期间,一些同学将要到A,B,C,D四个地方参加冬令营活动,现从这些同学中随机调查了一部分同学.根据调查结果,绘制成了如下两幅统计图: 
(1)扇形A的圆心角的度数为 , 若此次冬令营一共有320名学生参加,则前往C地的学生约有人,并将条形统计图补充完整;
(2)若某姐弟两人中只能有一人参加,姐弟俩决定用一个游戏来确定参加者:在4张形状、大小完全相同的卡片上分别写上﹣1,1,2,3四个整数,先让姐姐随机地抽取一张,再由弟弟从余下的三张卡片中随机地抽取一张.若抽取的两张卡片上的数字之和小于3则姐姐参加,否则弟弟参加.用列表法或树状图分析这种方法对姐弟俩是否公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个三角形的两条边长分别是1cm和2cm,一个内角为40度.
(1)请你借助图1画出一个满足题设条件的三角形;
(2)你是否还能画出既满足题设条件,又与(1)中所画的三角形不全等的三角形?若能,请你在图1的右边用“尺规作图”作出所有这样的三角形;若不能,请说明理由;
(3)如果将题设条件改为“三角形的两条边长分别是3cm和4cm,一个内角为40°”,那么满足这一条件,且彼此不全等的三角形共有几个.
友情提醒:请在你画的图中标出已知角的度数和已知边的长度,“尺规作图”不要求写作法,但要保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意解答
(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得线段BE、EF、FD之间的数量关系为 .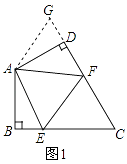
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF= ![]() ∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
(3)如图3,点A在点O的北偏西30°处,点B在点O的南偏东70°处,且AO=BO,点A沿正东方向移动249米到达E处,点B沿北偏东50°方向移动334米到达点F处,从点O观测到E、F之间的夹角为70°,根据(2)的结论求E、F之间的距离.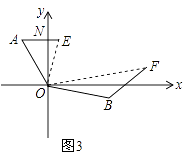
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④4ac﹣b2<0.其中正确结论有 . 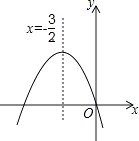
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB的垂直平分线分别交AB、BC于点M、P,AC的垂直平分线分别交AC、BC于点N、Q,∠BAC=110°,则∠PAQ=_____°.
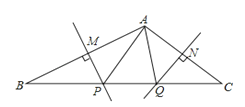
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个构造完全相同(除所标数字外)的转盘A、B,游戏规定:转动两个转盘各一次,指向大的数字获胜.
(1)用树状图或列表格列出两个转盘转出的所有可能出现的结果;
(2)如果由你和小明各选择一个转盘游戏,你会选择哪一个,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个安装有进出水管的30升容器,水管每单位时间内进出的水量是一定的,设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量![]() (升)与时间
(升)与时间![]() (分)之间的函数关系如图所示.根据图象回答下列问题:
(分)之间的函数关系如图所示.根据图象回答下列问题:
(1)求每分钟进水多少升;
(2)若12分钟后只放水,不进水,求需要多长时间可以把水放完;
(3)若从一开始进出水管同时打开,求需要多长时间可以将容器灌满。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com