
【题目】有一个安装有进出水管的30升容器,水管每单位时间内进出的水量是一定的,设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量![]() (升)与时间
(升)与时间![]() (分)之间的函数关系如图所示.根据图象回答下列问题:
(分)之间的函数关系如图所示.根据图象回答下列问题:
(1)求每分钟进水多少升;
(2)若12分钟后只放水,不进水,求需要多长时间可以把水放完;
(3)若从一开始进出水管同时打开,求需要多长时间可以将容器灌满。

【答案】(1)每分钟进水5升;(2)12分钟后只出水,不进水,需要8分钟可以把水放完;(3)需要24分钟可以将容器灌满。
【解析】
(1)由0—4分钟的进水总量即可求解;
(2)由4—12分钟的总进水量以及上一问所求解出的单位时间进水量即可求解;
(3)用容器容积除以单位时间进出水流量差即可.
(1)由图象可以看出在0-4分钟进水20升,故每分钟进水5升;
(2)有图象知4-12分钟进水10升,可以得出在4-12分钟出水30升;
所以每分钟出水3.75升,
30÷3.75=8(分钟)
所以12分钟后只出水,不进水,需要8分钟可以把水放完;
(3)进出水同时打开:
30÷(5-3.75)=24(分)
所以需要24分钟可以将容器灌满。


科目:初中数学 来源: 题型:
【题目】阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.
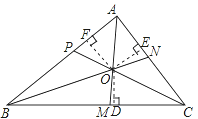
已知:如图,AM,BN,CP是△ABC的三条角平分线.
求证:AM、BN、CP交于一点.
证明:如图,设AM,BN交于点O,过点O分别作OD⊥BC,OF⊥AB,垂足分别为点D,E,F.
∵O是∠BAC角平分线AM上的一点( ),
∴OE=OF( ).
同理,OD=OF.
∴OD=OE( ).
∵CP是∠ACB的平分线( ),
∴O在CP上( ).
因此,AM,BN,CP交于一点.
查看答案和解析>>
科目:初中数学 来源: 题型:
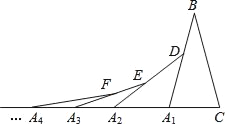
【题目】如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,第2017个三角形的底角度数是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( ) 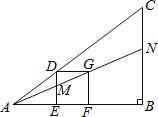
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两村在一条小河的同一侧,要在河边建一水厂向两村供水.
⑴.若要使自来水厂到两村的距离相等,厂址P应选在哪个位置?
⑵.若要使自来水厂到两村的输水管用料最省,厂址Q应选在哪个位置?请将上述两种情况下的自来水厂厂址标出,并保留作图痕迹.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是边BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③四边形AEPF的面积=△ABC的面积的一半,④当EF最短时,EF=AP,上述结论始终正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积进行了证明.著名数学家华罗庚提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
请根据图1中直角三角形叙述勾股定理.

以图1中的直角三角形为基础,可以构造出以a,b为底,以a+b为高的直角梯形(如图2).请你利用图2,验证勾股定理;
利用图2中的直角梯形,我们可以证明![]() .其证明步骤如下:
.其证明步骤如下:
∵BC=a+b,AD=_____;
又∵在直角梯形ABCD中有BC_____AD(填大小关系),即_____.
∴![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
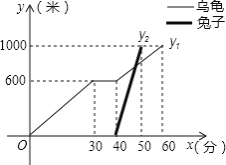
①兔子和乌龟同时从起点出发;
②“龟兔再次赛跑”的路程为1000米;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法共有____________个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com