
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

【答案】(1)证明见解析;(2)69°.
【解析】试题分析:(1)根据已知条件易证∠BEO=∠1,根据等式的性质可得∠AEC=∠BED,利用ASA即可证明△AEC≌△BED;(2)由△AEC≌△BED可得EC=ED,∠C=∠BDE;在△EDC中,根据等腰三角形的性质和三角形的内角和定理可求得∠C的度数,根据全等三角形的性质即可求得∠BDE的度数.
试题解析:
(1)证明:∵AE和BD相交于点O, ∴∠AOD=∠BOE.
在△AOD和△BOE中, ∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO, ∴∠AEC=∠BED.
在△AEC和△BED中,
∠A=∠B,AE=BE,∠AEC=∠BED,
∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中, ∵EC=ED,∠1=42°,
∴∠C=∠EDC=69°,
∴∠BDE=∠C=69°.


科目:初中数学 来源: 题型:
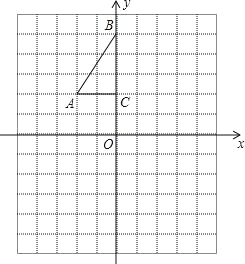
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(﹣2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(﹣2,﹣6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是( )
A.110°
B.100°
C.90°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.下列三个条件:①AB∥CD,②∠B=∠C.③∠E=∠F.从中任选两个作为条件,另一个作为结论,编一道数学题,并说明理由.
已知: ;
结论: ;
理由: 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是一角度为10°的钢架,要使钢架更加牢固,需在其内部添加一些钢管:EF、FG、GH…,且OE=EF=FG=GH…,在OA、OB足够长的情况下,最多能添加这样的钢管的根数为 _________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD,其中正确的有( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2= ( ),
又因为∠1=∠2,
所以∠1=∠3( ),
所以AB∥( ),
所以∠BAC+ =180°( ),
因为∠BAC=80°,
所以∠AGD= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com