
【题目】如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是( )
A.110°
B.100°
C.90°
D.80°
【答案】B
【解析】解:∵∠A+∠B+∠ADC+∠DCB=360°,∠A+∠B=200°,
∴∠ADC+∠DCB=160°.
又∵∠ADC、∠DCB的平分线相交于点O,
∴∠ODC=![]() ∠ADC,∠OCD=
∠ADC,∠OCD=![]() ,
,
∴∠ODC+∠OCD=80°,
∴∠COD=180°﹣(∠ODC+∠OCD)=100°.
故选B.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角,以及对多边形内角与外角的理解,了解多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°.


科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)的顶点为M,经过原点O且与x轴另一交点为A.
(1)求点A的坐标;
(2)若△AMO为等腰直角三角形,求抛物线C1的解析式;
(3)现将抛物线C1绕着点P(m,0)旋转180°后得到抛物线C2,若抛物线C2的顶点为N,当b=1,且顶点N在抛物线C1上时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学兴趣小组活动中,同学们做了一个找朋友的游戏:有六个同学A、B、C、D、E、F分别藏在六张大纸牌的后面,如图,A、B、C、D、E、F所持的纸牌的前面分别写有六个算式:66;63+63;(63)3;(2×62)×(3×63);(22×32)3;(64)3÷62 . 游戏规定:所持算式的值相等的两个人是朋友.如果现在由同学A来找他的朋友,他可以找谁呢?说说你的看法.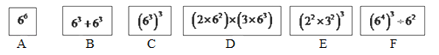
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=![]() 经过正方形AOBC对角线的交点,半径为
经过正方形AOBC对角线的交点,半径为![]() 的圆内切于△ABC,则k的值为( ).
的圆内切于△ABC,则k的值为( ).

A.![]() B.2 C.4 D.
B.2 C.4 D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com