
【题目】如图,已知抛物线y=x2﹣(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.
(1)求m的值;
(2)求A、B两点的坐标;
(3)当﹣3<x<1时,在抛物线上是否存在一点P,使得△PAB的面积是△ABC面积的2倍?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵抛物线的顶点在x轴上,
∴它与x轴只有一个交点,
∴(m+3)2﹣4×9=0,
解得m=3或m=﹣9,
又∵抛物线对称轴大于0
∴﹣ ![]() >0,即m>﹣3,
>0,即m>﹣3,
∴m=3;
(2)
解:由(1)可得抛物的解析式为y=x2﹣6x+9,
解方程组 ![]() ,
,
得 ![]() 或
或 ![]() ,
,
∴点A的坐标为(1,4),点B的坐标为(6,9);
(3)
解:存在,
设点P(a,b),如图,作PT⊥x轴交BD于点E,AR⊥x轴,BS⊥x轴,
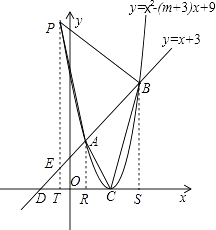
∵A(1,4),B(6,9),C(3,0),P(a,b)
∴AR=4,BS=9,RC=3﹣1=2,CS=6﹣3=3,RS=6﹣1=5,PT=b,RT=1﹣a,ST=6﹣a,
∴S△ABC=S梯形ARSB﹣S△ARC﹣S△BCS
= ![]() ×(4+9)×5﹣
×(4+9)×5﹣ ![]() ×2×4﹣
×2×4﹣ ![]() ×3×9
×3×9
=15,
S△PAB=S梯形PBST﹣S梯形ABSR﹣S梯形ARTP
= ![]() ×(9+b)(6﹣a)﹣
×(9+b)(6﹣a)﹣ ![]() ×(4+9)×5﹣
×(4+9)×5﹣ ![]() ×(b+4)(1﹣a)
×(b+4)(1﹣a)
= ![]() (5b﹣5a﹣15),
(5b﹣5a﹣15),
又∵S△PAB=2S△ABC,
∴ ![]() (5b﹣5a﹣15)=30,
(5b﹣5a﹣15)=30,
∴b﹣a=15,b=15+a,
∵点P在抛物线上
∴b=a2﹣6a+9,
∴15+a=a2﹣6a+9,
∴a2﹣7a﹣6=0,
解得:a= ![]() ,
,
∵﹣3<a<1,
∴a= ![]() ,
,
∴b=15+a= ![]() ,
,
∴P( ![]() ,
, ![]() ).
).
【解析】(1)由顶点在x轴上知它与x轴只有一个交点,即对应一元二次方程中△=0,可得关于m的方程,求解即可得m;(2)联立抛物线与直线解析式可得方程组,求解即可得A、B坐标;(3)设点P(a,b),作PT⊥x轴交BD于点E,AR⊥x轴,BS⊥x轴,分别表示出AR、BS、RC、CS、RS、PT、RT、ST的长,根据S△ABC=S梯形ARSB﹣S△ARC﹣S△BCS求出S△ABC , 由S△PAB=S梯形PBST﹣S梯形ABSR﹣S梯形ARTP表示出S△PAB , 根据△PAB的面积是△ABC面积的2倍可得a、b间关系,代入抛物线解析式即可求得.
【考点精析】掌握二次函数的图象是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
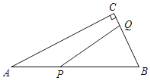
【题目】已知,如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=18cm.动点P从点A出发,沿AB向点B运动,动点Q从点B出发,沿BC向点C运动,如果动点P以2cm/s,Q以1cm/s的速度同时出发,设运动时间为t(s),解答下列问题:
(1)t为何值时,△PBQ是等边三角形?
(2)P,Q在运动过程中,△PBQ的形状不断发生变化,当t为何值时,△PBQ是直角三角形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波火车站北广场将于2015年底投入使用,计划在广场内种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D在同一条直线上,点E、F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
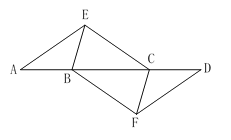
(1)求证:△ACE≌△DBF;
(2)求证:四边形BFCE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是半圆,连接AB,点O为AB的中点,点C,D在
是半圆,连接AB,点O为AB的中点,点C,D在 ![]() 上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( ) 
A.26°
B.28°
C.30°
D.32°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为:A(﹣2,3)、B(﹣6,0)、C(﹣1,0). 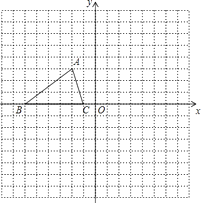
(1)将△ABC沿y轴翻折,画出翻折后的△A1B1C1 , 点A的对应点A1的坐标是
(2)△ABC关于x轴对称的图形△A2B2C2 , 直接写出点A2的坐标
(3)若△DBC与△ABC全等(点D与点A重合除外),请直接写出满足条件点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com