
【题目】如图,已知在△ABC中,AD⊥BC于点D,BE⊥AC于点E,且DF=DC。
(1)求证:BD=AD;
(2)若AF=1,DC=3,求BF的长.
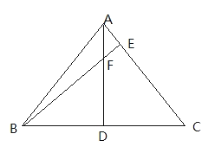
【答案】(1)证明见解析;(2)BF=5
【解析】
(1)、根据AD⊥BC和AC⊥BE得出∠EBC+∠C=90° ,∠CAD+∠C=90°,从而得出∠CAD=∠EBC,结合DF=DC得出△ACD和△BFD全等,从而得出答案;(2)、根据全等得出AF=1,DC=3,DF=DC,BD=AD=4,最后根据Rt△ADC的勾股定理求出AC的长度,即BF的长度.
(1)证明:∵ AD⊥BC,
∴ △ACD和△BFD是直角三角形 (两边相互垂直的三角形是直角三角形),∵ AC⊥BE,
∴ ∠BEC=90°,∴ ∠EBC+∠C=90°,∵ △ACD是直角三角形,
∴ ∠CAD+∠C=90° (直角三角形的两个锐角互余),
∵ ∠EBC+∠C=90° ,∠CAD+∠C=90°,∴ ∠CAD=∠EBC,∴ △ACD≌△BFD(AAS),
∴ BD=AD(全等三角形的对应边相等),
(2)、由(1)得△ACD≌△BFD, ∴BD=AD,AD=AC(全等三角形的对应边相等),
∵AF=1,DC=3,DF=DC, ∴BD=AD=4,又∵AD⊥BC,
∴AD2+DC2=AC2(勾股定理), ∴BF=AC=5.


科目:初中数学 来源: 题型:
【题目】某通讯公司推出A、B两种手机话费套餐,这两种套餐每月都有一定的固定费用和免费通话时间,超过免费通话时间的部分收费标准为:A套餐a元/分,B套餐b元/分,使用A、B两种套餐的通话费用y(元)与通话时间x(分)之间的函数图象如图所示.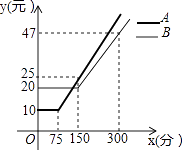
(1)当手机通话时间为50分钟时,写出A、B两种套餐的通话费用.
(2)求a,b的值.
(3)当选择B种套餐比A种套餐更合算时,求通话时间x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,E是AD边上一动点,AE=m,将△ABE沿BE折叠后得到△GBE.延长BG交直线CD于点F. 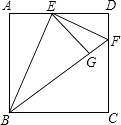
(1)若∠ABE:∠BFC=n,则n=;
(2)当E运动到AD中点时,求线段GF的长;
(3)若限定F仅在线段CD上(含端点)运动,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,等腰直角三角形的直角边BC在x轴正半轴上滑动,点C的坐标为(t,0),直角边AC=4,经过O,C两点做抛物线y1=ax(x﹣t)(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)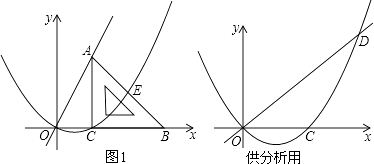
(1)填空:用含t的代数式表示点A的坐标及k的值:A , k=;
(2)随着三角板的滑动,当a= ![]() 时:
时:
①请你验证:抛物线y1=ax(x﹣t)的顶点在函数y= ![]() 的图象上;
的图象上;
②当三角板滑至点E为AB的中点时,求t的值;
(3)直线OA与抛物线的另一个交点为点D,当t≤x≤t+4,|y2﹣y1|的值随x的增大而减小,当x≥t+4时,|y2﹣y1|的值随x的增大而增大,求a与t的关系式及t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长( )
A. ![]() cm B.
cm B. ![]() cm C. 12cm D. 13cm
cm C. 12cm D. 13cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把平面内与一个定点F和一条定直线l(l不经过点F)距离相等的点的轨迹(满足条件的所有点所组成的图形)叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.
(1)已知抛物线的焦点F(0, ![]() ),准线l:
),准线l: ![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)已知抛物线的解析式为:y=x2﹣n2 , 点A(0, ![]() )(n≠0),B(1,2﹣n2),P为抛物线上一点,求PA+PB的最小值及此时P点坐标;
)(n≠0),B(1,2﹣n2),P为抛物线上一点,求PA+PB的最小值及此时P点坐标;
(3)若(2)中抛物线的顶点为C,抛物线与x轴的两个交点分别是D、E,过C、D、E三点作⊙M,⊙M上是否存在定点N?若存在,求出N点坐标并指出这样的定点N有几个;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ACB=90°,AC=BC,BD⊥DE,AE⊥DE,垂足分别为D、E.(这几何模型具备“一线三直角”)如下图:
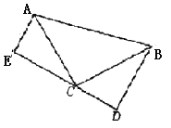
(1)①请你证明:△ACE≌△CBD;②若AE=3,BD=5,求DE的长;
(2)迁移:如图:在等腰Rt△ABC中,且∠C=90°,CD=2,BD=3,D、E分别是边BC,AC上的点,将DE绕点D顺时针旋转90°,点E刚好落在边AB上的点F处,则CE=________。(不要求写过程)
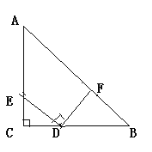
查看答案和解析>>
科目:初中数学 来源: 题型:
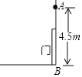
【题目】如图,有一个由传感器A控制的灯,要装在门上方离地面4.5m的墙上,任何东西只要移至该灯5m及5m内,灯就会自动发光,小明身高1.5m,他走到离墙_______的地方灯刚好发光.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com