
����Ŀ��ijͨѶ��˾�Ƴ�A��B�����ֻ������ײͣ��������ײ�ÿ�¶���һ���Ĺ̶����ú����ͨ��ʱ�䣬�������ͨ��ʱ��IJ����շѱ�Ϊ��A�ײ�aԪ/�֣�B�ײ�bԪ/�֣�ʹ��A��B�����ײ͵�ͨ������y��Ԫ����ͨ��ʱ��x���֣�֮��ĺ���ͼ����ͼ��ʾ��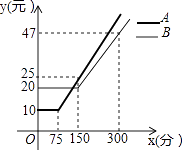
��1�����ֻ�ͨ��ʱ��Ϊ50����ʱ��д��A��B�����ײ͵�ͨ�����ã�
��2����a��b��ֵ��
��3����ѡ��B���ײͱ�A���ײ�����ʱ����ͨ��ʱ��x��ȡֵ��Χ��
���𰸡�
��1��
�⣺��ͼ���֪�����ֻ�ͨ��ʱ��Ϊ50����ʱ��A��B�����ײ͵�ͨ�����÷ֱ�Ϊ10Ԫ��20Ԫ��
��2��
�⣺a= ![]() =0.2��b=
=0.2��b= ![]() =0.18��
=0.18��
���ԣ�a��b��ֵ�ֱ���0.2��0.18��
��3��
�⣺A���ײͳ������ʱ��y��x�ĺ�����ϵʽΪy=0.2x��5��x��75����
��ͼ���֪����75��x��150ʱ����A��B�����ײ͵�ͨ������ͬ����0.2x��5=20��
���x=125��
�൱x��125ʱ��ѡ��B���ײ����㣮
����������1������ͼ����ã���2�����ݴ���ϵ����������ã���3�����������շ���ͬ�г����̣���⣬�����շ���ͬ��ʱ��ѡ��B�ײͣ�
�����㾫�������ڱ��⿼���ȷ��һ�κ����ı���ʽ����Ҫ�˽�ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ�������ܵó���ȷ�𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OABC��һ�ŷ���ƽ��ֱ������ϵ�еľ���ֽƬ��OΪԭ�㣬��A��x����������ϣ���C��y����������ϣ�OA=10��OC=8����OC����ȡһ��D����ֽƬ��AD���ۣ�ʹ��O����BC���ϵĵ�E������D��E��������꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���F�ڱ�BC�ϣ���AF=AD������D��DE��AF������Ϊ��E�� 
��1����֤��DE=AB��
��2����DΪԲ�ģ�DEΪ�뾶��Բ����AD�ڵ�G����BF=FC=1������ ![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڱ߳�Ϊ1��С��������ɵ������������н�����ͼ��ʾ��ƽ��ֱ������ϵ����֪���������ABC�������ε��������㶼��С�����εĶ����ϣ�.

��1�����ABC�������_______.
��2��������ABC����y��ԳƵġ�A1B1C1.
��3��д����B����ԳƵ�B1������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ת�任��ȫ�ȱ任��һ����ʽ�������ڽ���ʵ���о�������ת�任�ķ���������ȫ����������������⡣
��1������̽������ͼ�٣��ڡ�ABC�У���BAC=90�㣬AB=AC����D��E�ڱ�BC�ϣ���DAE=45��

��̽���߶�BD��CE��DE�������ʲô���������Ρ����ǿ��Թ���B��BF��BC��ʹBF=EC������AF��DF���á�AFB=45������õ���AFB�ա�AEC���൱�ڰѡ�AEC�Ƶ�A˳ʱ����ת90�㵽��AFB����������������������̣�
�ߡ�AFB�ա�AEC��
���BAF= ��AF=AE��
�ߡ�BAC=90�㣬��DAE=45�㣬
���BAD+��CAE= ��
���BAF+��BAD=45�㣬
���DAF=45��= ��
�ڡ�DAF���DAE����
AF=AE��
��DAF=��DAE��
AD=AD��
���DAF�ա�DAE��
��DF= ��
��BD��BF��DF���ֱ����������
��BD��CE��DE���ֱ��������.
��2����������
�� ��ͼ�ڣ����ı���ABCD�У�AB=AD����BAD=��BCD=90�㣬��ABC+��ADC=180�㣬��E�ڱ�BC�ϣ���F�ڱ�CD�ϣ���EAF=45�����ж��߶�BE��DF��EF֮���������ϵ����˵�����ɡ�
�� ��ͼ�ۣ��ڢٵĻ���������E��F�ֱ���BC��CD���ӳ��ߣ������������䣬���еĹ�ϵ��ͼ�����Ƿ���Ȼ��������������˵�����ɣ�����������д���µĹ�ϵ����˵�����ɡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�CD�ǡ�ACB�Ľ�ƽ���ߣ�CE��AB���ϵĸߣ�
��1������A=40������B=60�������DCE�Ķ�����
��2������A=m����B=n�����DCE������m��n��ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AD��BC��D����BD=AD��FD=CD.
��1����֤����FBD=��CAD��
��2����֤��BE��AC.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪AE��AB��AF��AC��AE=AB��AF=AC�����ж��߶�EC��BF�Ĺ�ϵ��֤����
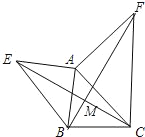
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
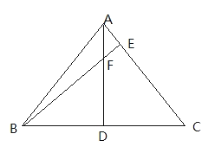
����Ŀ����ͼ����֪����ABC�У�AD��BC�ڵ�D��BE��AC�ڵ�E����DF=DC��
(1)��֤��BD=AD��
(2)��AF=1��DC=3����BF�ij�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com