
【题目】如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,
(1)若∠A=40°,∠B=60°,求∠DCE的度数.
(2)若∠A=m,∠B=n,求∠DCE.(用m、n表示)

【答案】(1)10度;(2)![]()
【解析】试题分析:
(1)由已知易得∠ACB=80°,∠AEC=90°,由CD平分∠ACB可得∠ACD=40°,由∠AEC=90°、∠A=40°可得∠ACE=50°,这样就可得∠DCE=∠ACE-∠ACD=10°;
(2)把(1)中∠A=40°,∠B=60°分别换成m和n即可用含m、n的式子表达出∠DCE.
试题解析:
(1)∵△ABC中,∠A=40°,∠B=60°,
∴∠ACB=180°-40°-60°=80°,
又∵CD是∠ACB的角平分线,CE是AB边上的高,
∴∠ACD=![]() ∠ACB=40°,∠ACE=90°﹣∠A=50°,
∠ACB=40°,∠ACE=90°﹣∠A=50°,
∴∠DCE=∠ACE﹣∠ACD=50°﹣40°=10°;
(2)∵△ABC中,∠A=m,∠B=n,
∴∠ACB=180°﹣m﹣n,
又∵CD是∠ACB的角平分线,CE是AB边上的高,
∴∠ACD=![]() ∠ACB=
∠ACB=![]() ,∠ACE=90°﹣∠A=90°﹣m,
,∠ACE=90°﹣∠A=90°﹣m,
∴∠DCE=∠ACE﹣∠ACD=(90°﹣m)﹣![]() =
=![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将坐标是(-5,0),(-4,-2),(-3,0),(-2,-2),(-1,0)的点用线段依次连接起来形成一个图案Ⅰ.
(1)作出该图案关于y轴对称的图案Ⅱ;
(2)将所得到的图案Ⅱ沿x轴向上翻折180°后得到一个新图案Ⅲ,试写出它的各顶点的坐标;
(3)观察图案Ⅰ与图案Ⅲ,比较各顶点的坐标和图案位置,你能得到什么结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把两个大小相等,形状相同的两个三角形称之为全等三角形,如果两个三角形仅仅是形状相同,我们可以称之为相似三角形,如图①△ABC与△DEF形状相同,我们就可以说△ABC 与△DEF相似,记作△ABC∽△DEF,点A与点D、点B与点E、点C与点F分别是对应点。下面我们就相似三角形的知识进行一些简单的探索。

(1)观察下列图②两组图形,相似的一组是 。

(2)如图③,小明用一张纸遮住了3个三角形的一部分,你是可以画出这3个三角形的。

提出问题:①如图,如果∠A=∠C,∠B=∠D,AB=CD,那么第一个三角形与第二个三角形全等吗?你的判断是 ,(填“是”或“否”)判断的依据是 。
②如图,如果∠A=∠E,∠B=∠F,2AB=EF,那么第一个三角形与第三个三角形相似吗?你的判断是 ,(填“是”或“否”)
(3)由(1)、(2)你可以得出的结论是:有 个角分别相等的两个三角形相似。
(4)用(3)的结论解决下面两个问题.
①已知:如图,AB∥CD。AD与BC相交于点O,试说明△ABO∽△DCO。
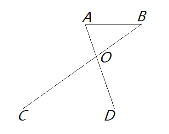
②已知:如图,在△ABC中,点D、E、F分别在边BC、AB、AC上,∠B=∠C=∠EDF,试说明△BDE∽△CFD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出A、B两种手机话费套餐,这两种套餐每月都有一定的固定费用和免费通话时间,超过免费通话时间的部分收费标准为:A套餐a元/分,B套餐b元/分,使用A、B两种套餐的通话费用y(元)与通话时间x(分)之间的函数图象如图所示.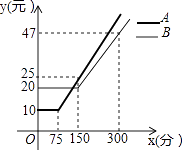
(1)当手机通话时间为50分钟时,写出A、B两种套餐的通话费用.
(2)求a,b的值.
(3)当选择B种套餐比A种套餐更合算时,求通话时间x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块等腰直角的三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,使A、C、B′三点共线,那么旋转角度的大小为( )
A.45°
B.90°
C.120°
D.135°
查看答案和解析>>
科目:初中数学 来源: 题型:
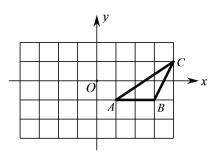
【题目】如图,△ABC 顶点的坐标分别为 A (1,-1)、B(3,-1)、C(4,1).
⑴将△ABC向上平移1个单位,再向左平移1个单位,请画出平移后得到的△A1B1C1并写出点 A1、B1、C1 的坐标;
⑵若△A1B1C1 与△A1B1D 全等(D 点与 C1 不重合),直接写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把平面内与一个定点F和一条定直线l(l不经过点F)距离相等的点的轨迹(满足条件的所有点所组成的图形)叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.
(1)已知抛物线的焦点F(0, ![]() ),准线l:
),准线l: ![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)已知抛物线的解析式为:y=x2﹣n2 , 点A(0, ![]() )(n≠0),B(1,2﹣n2),P为抛物线上一点,求PA+PB的最小值及此时P点坐标;
)(n≠0),B(1,2﹣n2),P为抛物线上一点,求PA+PB的最小值及此时P点坐标;
(3)若(2)中抛物线的顶点为C,抛物线与x轴的两个交点分别是D、E,过C、D、E三点作⊙M,⊙M上是否存在定点N?若存在,求出N点坐标并指出这样的定点N有几个;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com