
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是双曲线y1= ![]() 与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO= ![]() .
. 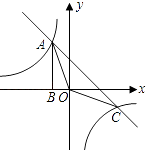
(1)求这两个函数的解析式;
(2)求△AOC的面积;
(3)直接写出使y1>y2成立的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,下列结论正确的有( )
①AD=BD=BC;②△BCD≌△ABC;③AD2=ACDC;④点D是AC的黄金分割点.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图所示,AB//CD,点E在AD的延长线上,∠EDC与∠B互为补角.
(1)问AD,BC是否平行?请说明理由;
(2)如果∠EDC=72°,∠1=∠2=2∠CAB,求∠CAF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN//直线PQ,点A、B分别是直线MN、PQ上的两点.将射线AM绕点A顺时针匀速旋转,射线BQ绕点B顺时针匀速旋转,旋转后的射线分别记为AM′、BQ′,已知射线AM、射线BQ旋转的速度之和为7度/秒.
(1)如果射线BQ 先转动30°后,射线AM、BQ′再同时旋转10秒时,射线AM′与BQ′第一次出现平行.求射线AM、BQ的旋转速度;
(2)若射线AM、BQ分别以(1)中速度同时转动t秒,在射线AM′与AN重合之前,求t为何值时AM′⊥BQ′;
(3)若∠BAN=45°,射线AM、BQ分别以(1)中的速度同时转动t秒,在射线AM′与AN重合之前,射线AM′与BQ′交于点H,过点H作HC⊥PQ,垂足为C,如图2所示,设∠BAH=α,∠BHC=β,求α和β满足的数量关系,直接写出结果.
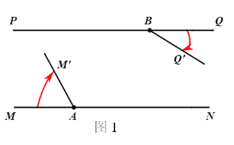


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民公园划出一块矩形区域,用以栽植鲜花.
(1)经测量,该矩形区域的周长是72m,面积为320m2 , 请求出该区域的长与宽;
(2)公园管理处曾设想使矩形的周长和面积分别为(1)中区域的周长和面积的一半,你认为此设想合理吗?如果此设想合理,请求出其长和宽;如果不合理,请说明理由,并求出在(1)中周长减半的条件下矩形面积的最大值. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“春节”是我国的传统佳节,民间历来有吃“汤圆”的习俗.某食品厂为了解市民对去年销量较好的肉馅(A)、豆沙馅 (B)、菜馅(C)、三丁馅 (D)四种不同口味汤圆的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).请根据以上信息回答:
(1)本次参加抽样调查的居民人数是 人;
(2)将图 ①②补充完整;( 直接补填在图中)
(3)求图②中表示“A”的圆心角的度数;
(4)若居民区有8000人,请估计爱吃D汤圆的人数.
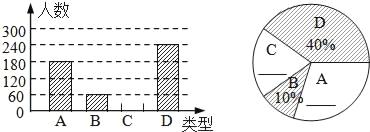
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF:FC=( ) 
A.1:4
B.1:3
C.1:2
D.1:1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com