
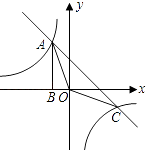
【题目】如图,Rt△ABO的顶点A是双曲线y1= ![]() 与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO= ![]() .
. 
(1)求这两个函数的解析式;
(2)求△AOC的面积;
(3)直接写出使y1>y2成立的x的取值范围.
【答案】
(1)解:设A点坐标为(x,y),且x<0,y>0,
则S△ABO= ![]() |BO||BA|=
|BO||BA|= ![]() (﹣x)y=
(﹣x)y= ![]() ,
,
∴xy=﹣3,
又∵y= ![]() ,
,
即xy=k,
∴k=﹣3.
∴所求的两个函数的解析式分别为y=﹣ ![]() ,y=﹣x+2
,y=﹣x+2
(2)解:由y=﹣x+2,
令x=0,得y=2.
∴直线y=﹣x+2与y轴的交点D的坐标为(0,2),
∵A、C在反比例函数的图象上,
∴ 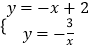 ,解得
,解得 ![]() ,
, ![]() ,
,
∴交点A为(﹣1,3),C为(3,﹣1),
∴S△AOC=S△ODA+S△ODC= ![]() OD(|x1|+|x2|)=
OD(|x1|+|x2|)= ![]() ×2×(3+1)=4
×2×(3+1)=4
(3)解:使y1>y2成立的x的取值范围是:﹣1<x<0或x>3
【解析】(1)欲求这两个函数的解析式,关键求k值.根据反比例函数性质,k绝对值为3且为负数,由此即可求出k;(2)由函数的解析式组成方程组,解之求得A、C的坐标,然后根据S△AOC=S△ODA+S△ODC即可求出;(3)根据图象即可求得.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求:

(1)斜边AB的长;
(2)△ABC的面积;
(3)高CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.
(1)求证:DF=AE;
(2)当AB=2时,求BE2的值.
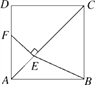
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() ﹣1来表示
﹣1来表示![]() 的小数部分,因为
的小数部分,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.请解答:
的整数部分是1,将这个数减去其整数部分,差就是小数部分.请解答:
(1)![]() 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;
(2)如果![]() 的小数部分为a,
的小数部分为a,![]() 的整数部分为b,求a+b﹣
的整数部分为b,求a+b﹣![]() 的值;
的值;
(3)已知:10+![]() =x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
=x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙. 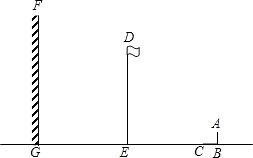
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC,BD相交于点O,AC平分∠DCB,CD⊥AD,∠ACD=45°,∠BAC=60°.
(1)证明:AD∥BC;
(2)求∠EAD的度数;
(3)求证:∠AOB=∠DAC +∠CBD

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

查看答案和解析>>
科目:初中数学 来源: 题型:
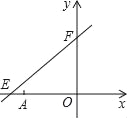
【题目】如图,直线y=![]() x+6与x轴、y轴分别相交于点E、F,点A的坐标为(﹣6,0),P(x,y)是直线y=
x+6与x轴、y轴分别相交于点E、F,点A的坐标为(﹣6,0),P(x,y)是直线y=![]() x+6上一个动点.
x+6上一个动点.
(1)在点P运动过程中,试写出△OPA的面积s与x的函数关系式;
(2)当P运动到什么位置,△OPA的面积为![]() ,求出此时点P的坐标;
,求出此时点P的坐标;
(3)过P作EF的垂线分别交x轴、y轴于C、D.是否存在这样的点P,使△COD≌△FOE?若存在,直接写出此时点P的坐标(不要求写解答过程);若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com