
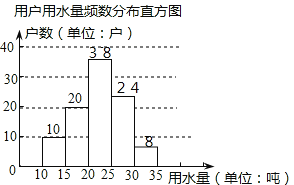
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?

【答案】(1)100;(2)补图见解析;(3)39600户.
【解析】试题分析:(1)根据统计图可知“10吨~15吨”的用户10户占10%,从而可以求得此次调查抽取的户数;
(2)根据(1)中求得的用户数与条形统计图可以得到“15吨~20吨”的用户数,进而求得扇形图中“15吨~20吨”部分的圆心角的度数;
(3)根据前面统计图的信息可以得到该地区20万用户中约有多少用户的用水全部享受基本价格.
试题解析:(1)此次调查抽取的用户户数为:10÷10%=100(户)
(2)用水量在15-20吨之间的用户数量:100-(10+36+25+9)=100-80=20
补全频数分布直方图
扇形图中“15吨~20吨”部分的圆心角的度数: ![]()
(3)少于25吨的有10+20+38=68(户)
∴少于25吨的户数是:![]() (万户)
(万户)


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.

(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索题
图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.

(1)你认为图b中的影部分的正方形的边长等于 .
(2)请用两种不同的方法求图b中阴影部分的面积.
方法1: (只列式,不化简)
方法2: (只列式,不化简)
(3)观察图b你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2,(m-n)2,![]() .
.
(4)根据(3)题中的等量关系,解决如下问题:若a+b=8,ab=5,则 (a-b)2= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“南”、“山”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“南山”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是双曲线y1= ![]() 与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO= ![]() .
. 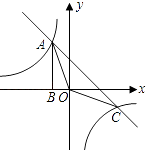
(1)求这两个函数的解析式;
(2)求△AOC的面积;
(3)直接写出使y1>y2成立的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
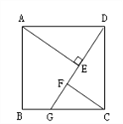
【题目】四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE⊥DG于E,CF∥AE交DG于F.
(1) 在图中找出一对全等三角形,并加以证明;
(2)求证:AE=FC+EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,下列结论正确的有( )
①AD=BD=BC;②△BCD≌△ABC;③AD2=ACDC;④点D是AC的黄金分割点.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
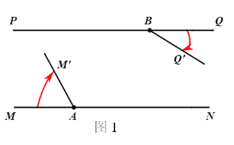
【题目】如图1,直线MN//直线PQ,点A、B分别是直线MN、PQ上的两点.将射线AM绕点A顺时针匀速旋转,射线BQ绕点B顺时针匀速旋转,旋转后的射线分别记为AM′、BQ′,已知射线AM、射线BQ旋转的速度之和为7度/秒.
(1)如果射线BQ 先转动30°后,射线AM、BQ′再同时旋转10秒时,射线AM′与BQ′第一次出现平行.求射线AM、BQ的旋转速度;
(2)若射线AM、BQ分别以(1)中速度同时转动t秒,在射线AM′与AN重合之前,求t为何值时AM′⊥BQ′;
(3)若∠BAN=45°,射线AM、BQ分别以(1)中的速度同时转动t秒,在射线AM′与AN重合之前,射线AM′与BQ′交于点H,过点H作HC⊥PQ,垂足为C,如图2所示,设∠BAH=α,∠BHC=β,求α和β满足的数量关系,直接写出结果.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1.
(1)如果点A,D表示的数互为相反数,那么点B表示的数是多少?
(2)如果点B,D表示的数互为相反数,那么图中表示的四个点中,哪一点表示的数的绝对值最大?为什么?
(3)当点B为原点时,若存在一点M到A的距离是点M到D的距离的2倍,则点M所表示的数是 .
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com