
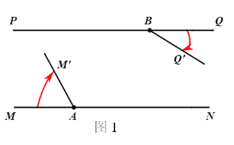
【题目】如图1,直线MN//直线PQ,点A、B分别是直线MN、PQ上的两点.将射线AM绕点A顺时针匀速旋转,射线BQ绕点B顺时针匀速旋转,旋转后的射线分别记为AM′、BQ′,已知射线AM、射线BQ旋转的速度之和为7度/秒.
(1)如果射线BQ 先转动30°后,射线AM、BQ′再同时旋转10秒时,射线AM′与BQ′第一次出现平行.求射线AM、BQ的旋转速度;
(2)若射线AM、BQ分别以(1)中速度同时转动t秒,在射线AM′与AN重合之前,求t为何值时AM′⊥BQ′;
(3)若∠BAN=45°,射线AM、BQ分别以(1)中的速度同时转动t秒,在射线AM′与AN重合之前,射线AM′与BQ′交于点H,过点H作HC⊥PQ,垂足为C,如图2所示,设∠BAH=α,∠BHC=β,求α和β满足的数量关系,直接写出结果.


【答案】(1) 射线AM、BQ的旋转速度分别为5度/秒、2度/秒;(2) 30秒;(3) 当![]() 时,
时,![]() 45°.
45°.
【解析】(1)设射线AM、BQ的旋转速度分别为x度/秒、y度/秒,根据速度之和等于7,以及射线AM、BQ的旋转角度相等列方程组求解即可;
(2)根据AM′与BQ′垂直,可得![]() ,求解即可;
,求解即可;
(3)根据题意得![]() ,延长AM′与BQ交于M′,易得∠A M′B=45°-α,∠HBC=90°-β,而A M′⊥BQ′,从而求得结论.
,延长AM′与BQ交于M′,易得∠A M′B=45°-α,∠HBC=90°-β,而A M′⊥BQ′,从而求得结论.
(1)设射线AM、BQ的旋转速度分别为x度/秒、y度/秒,根据题意得:
![]() ,解得
,解得![]()
答:射线AM、BQ的旋转速度分别为5度/秒、2度/秒.
(2)由AM′与BQ′垂直,则![]() ,
,
![]() ,
,
答:30秒时AM′⊥BQ′
(3)易得![]() ,如图,延长AM′与BQ交于M′,
,如图,延长AM′与BQ交于M′,
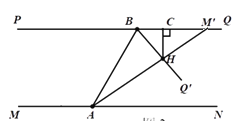
∵PQ∥MN,
∴∠AM′B=∠N AM′=45°-α,
∵HC⊥PQ,
∴∠HBC=90°-∠BHC=90°-β,
又AM′⊥BQ′,
∴∠HBC+∠AM′B=90°,
∴90°-β+45°-α=90°,即α+β=45°.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2 ![]() ,
, ![]() ,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q. 
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 如果![]() ,则
,则 ![]()
B. 如果|a|=|b|,那么a=b
C. 两个锐角的和是钝角
D. 如果一点到线段两端的距离相等,那么这点是这条线段的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把带有指针的圆形转盘A、B分别分成4等份、3等份的扇形区域,并在每一个小区域内标上数字(如图所示).小明、小乐两个人玩转盘游戏,游戏规则是:同时转动两个转盘,当转盘停止时,若指针所指两区域的数字之积为3的倍数,则小明胜;否则,小乐胜.(若有指针落在分割线上,则无效,需重新转动转盘) 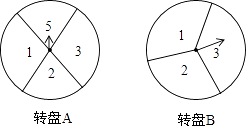
(1)试用列表或画树状图的方法,求小明获胜的概率;
(2)请问这个游戏规则对小明、小乐双方公平吗?做出判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E,F分别在边DC,AB上,DE=BF,把平行四边形沿直线EF折叠,使得点B,C分别落在B′,C′处,线段EC′与线段AF交于点G,连接DG,B′G.
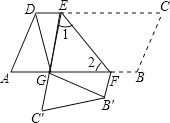
求证:(1)∠1=∠2;
(2)DG=B′G.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于频率与概率有下列几种说法:
①“明天下雨的概率是 90%”表示明天下雨的可能性很大;
②“抛一枚硬币正面朝上的概率为”表示每抛两次就有一次正面朝上;
③“某彩票中奖的概率是 1%”表示买 10 张该种彩票不可能中奖;
④“抛一枚硬币正面朝上的概率为![]() ”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在![]() 附近.
附近.
正确的说法是( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com