
【题目】探索题
图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.

(1)你认为图b中的影部分的正方形的边长等于 .
(2)请用两种不同的方法求图b中阴影部分的面积.
方法1: (只列式,不化简)
方法2: (只列式,不化简)
(3)观察图b你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2,(m-n)2,![]() .
.
(4)根据(3)题中的等量关系,解决如下问题:若a+b=8,ab=5,则 (a-b)2= .
【答案】(1)m-n;(2)(m+n)2-4mn;(m-n)2;(3)(m-n)2=(m+n)2-4mn;(4)44 .
【解析】(1)直接利用图b得出正方形的边长;
(2)利用已知图形结合边长为m+n的大正方形的面积减去长为m,宽为n的4个长方形面积以及边长为m﹣n的正方形的面积,分别求出答案;
(3)利用(2)中所求得出答案;
(4)利用(3)中关系式,将已知变形得出答案.
(1)阴影部分的正方形边长是:m﹣n.
故答案为:m﹣n;
(2)阴影部分的面积就等于边长为m﹣n的小正方形的面积,
方法1:边长为m+n的大正方形的面积减去长为2m,宽为2n的长方形面积,即(m+n)2﹣4mn;
方法2:边长为m﹣n的正方形的面积,即(m﹣n)2;
(3)由题意可得:(m-n)2=(m+n)2-4mn.
故答案为:(m-n)2=(m+n)2-4mn.
(4)∵a+b=8,ab=5,∴(a+b)2=64,∴(a﹣b)2+4ab=64,∴(a﹣b)2=64﹣4×5=44.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点O(0,0),A(1,0),B(1,1),C(2,0),△OBC的面积记为S1 , 过O、B、C三点的半圆面积记为S2;过O、B、C三点的抛物线与x轴所围成的图形面积记为S3 , 则S1、S2、S3的大小关系是 . (用“>”连接)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2 ![]() ,
, ![]() ,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q. 
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
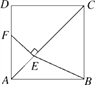
【题目】如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.
(1)求证:DF=AE;
(2)当AB=2时,求BE2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】回答下列问题:
(1)计算:①(x+2)(x+3)= ;② (x +7)( x-10)= ;③(x-5)(x-6)= .
(2)总结公式:(x+a)(x+b)= .
(3)已知a,b,m均为整数,且(x+a)(x+b)=x2+mx+6,求m的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() ﹣1来表示
﹣1来表示![]() 的小数部分,因为
的小数部分,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.请解答:
的整数部分是1,将这个数减去其整数部分,差就是小数部分.请解答:
(1)![]() 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;
(2)如果![]() 的小数部分为a,
的小数部分为a,![]() 的整数部分为b,求a+b﹣
的整数部分为b,求a+b﹣![]() 的值;
的值;
(3)已知:10+![]() =x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
=x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E,F分别在边DC,AB上,DE=BF,把平行四边形沿直线EF折叠,使得点B,C分别落在B′,C′处,线段EC′与线段AF交于点G,连接DG,B′G.
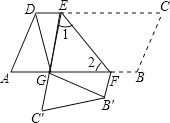
求证:(1)∠1=∠2;
(2)DG=B′G.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com