
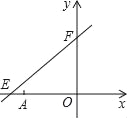
����Ŀ����ͼ��ֱ��y=![]() x+6��x�ᡢy��ֱ��ཻ�ڵ�E��F����A������Ϊ����6��0����P��x��y����ֱ��y=
x+6��x�ᡢy��ֱ��ཻ�ڵ�E��F����A������Ϊ����6��0����P��x��y����ֱ��y=![]() x+6��һ�����㣮
x+6��һ�����㣮
��1���ڵ�P�˶������У���д����OPA�����s��x�ĺ�����ϵʽ��
��2����P�˶���ʲôλ�ã���OPA�����Ϊ![]() �������ʱ��P�����ꣻ
�������ʱ��P�����ꣻ
��3����P��EF�Ĵ��߷ֱ�x�ᡢy����C��D���Ƿ���������ĵ�P��ʹ��COD�ա�FOE�������ڣ�ֱ��д����ʱ��P�����꣨��Ҫ��д�����̣����������ڣ���˵�����ɣ�
���𰸡���1��s=![]() x+18��x����8����s=��
x+18��x����8����s=��![]() x��18��x����8������2������6.5��
x��18��x����8������2������6.5�� ![]() ����9.5����1.125����3������P�㣬ʹ��COD�ա�FOE��P�������ǣ���
����9.5����1.125����3������P�㣬ʹ��COD�ա�FOE��P�������ǣ���![]() ��
�� ![]() ����
����![]() ��
�� ![]() ����
����
�����������������
��1������֪�����ɵ�OA=6�����P������Ϊ![]() �����P��OA�ľ���Ϊ
�����P��OA�ľ���Ϊ![]() ���ֵ�P�ڵ�һ�������͵���������������ֱ��������S��x��Ĺ�ϵʽ���ɣ�
���ֵ�P�ڵ�һ�������͵���������������ֱ��������S��x��Ĺ�ϵʽ���ɣ�
��2����S=![]() ���루1�������ù�ϵʽ�����x��ֵ������ö�Ӧ�ĵ�P�����ꣻ
���루1�������ù�ϵʽ�����x��ֵ������ö�Ӧ�ĵ�P�����ꣻ
��3����ͼ���ֵ�D��y��������������������������֪�������ۼ��㼴����ö�Ӧ�ĵ�P������.
���������
��1���ߵ�A������Ϊ��-6��0����
��OA=6��
����P��ֱ��![]() ����
����
�������P������Ϊ![]() ��
��
��ֱ��![]() ��x�ύ�ڵ�E����y�ύ�ڵ�F��
��x�ύ�ڵ�E����y�ύ�ڵ�F��
����E��F������ֱ�Ϊ��-8��0���ͣ�0��6����
�൱��P�ڵ�һ��������ʱ����OPA�����S=![]() ��OA��
��OA��![]() =
=![]() ��
��
����P�ڵ�������ʱ����OPA�����S=![]() ��OA��
��OA��![]() =
=![]() ��
��
���P�˶������У���OPA�����s��x�ĺ�����ϵʽ��S=![]() ��S=
��S=![]() ��
��
��2����S=![]() ����S=
����S=![]() ��S=
��S=![]() �ã�
�ã�
![]() ��
��![]() ��
��
����� ![]() ��
��![]() ��
��
����P������Ϊ![]() ��
��![]() ��
��
��3���������P�㣬ʹ��COD�ա�FOE����OD=OE=8��OC=OF=6��
����ͼ������D��y��ĸ�����ʱ����C��x��ĸ����ᣬ
��OD=8��OC=6��
����D��C������ֱ�Ϊ��0��-8���ͣ�-6��0��,
��ֱ��CD�Ľ���ʽΪ��y=kx+b���� ![]() �����
�����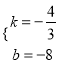 ��
��
��![]() ��
��
��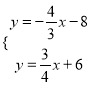 ��ã�
��ã� 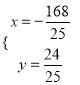 ��
��
����P������Ϊ![]() ��
��
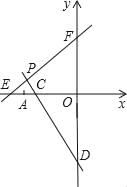
������ͼ��ʾ������D��y��������ʱ����C��x��������ᣬͬ���ɽ�ô�ʱ��P������Ϊ![]() ��
��
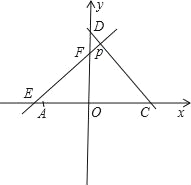
��������������P�㣬ʹ��COD�ա�FOE��P��������![]() ��
��![]() ��
��


 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABO�Ķ���A��˫����y1= ![]() ��ֱ��y2=��x����k+1���ڵڶ����Ľ��㣮AB��x����B����S��ABO=
��ֱ��y2=��x����k+1���ڵڶ����Ľ��㣮AB��x����B����S��ABO= ![]() ��
�� 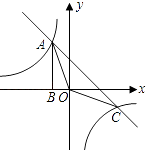
��1���������������Ľ���ʽ��
��2�����AOC�������
��3��ֱ��д��ʹy1��y2������x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������һ���������������ֲ�ʻ���
��1�����������þ���������ܳ���72m�����Ϊ320m2 �� �����������ij������
��2����������������ʹ���ε��ܳ�������ֱ�Ϊ��1����������ܳ��������һ�룬����Ϊ�������������������������������䳤�Ϳ����������������˵�����ɣ�������ڣ�1�����ܳ�����������¾�����������ֵ�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
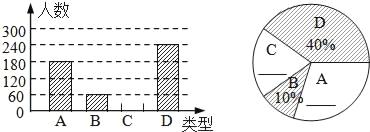
����Ŀ�������ڡ����ҹ��Ĵ�ͳ�ѽڣ���������гԡ���Բ����ϰ�ף�ijʳƷ��Ϊ�˽������ȥ�������Ϻõ����ڣ�A������ɳ�� ��B�������ڣ�C���������� ��D�����ֲ�ͬ��ζ��Բ��ϲ��������ڽ�ǰ��ij��������������˳������飬��������������Ƴ���������ͳ��ͼ���в��������������������Ϣ�ش�
��1�����βμӳ�������ľ����������� ���ˣ�
��2����ͼ �٢������������� ֱ�Ӳ�����ͼ�У�
��3����ͼ���б�ʾ��A����Բ�ĽǵĶ�����
��4������������8000�ˣ�����ư���D��Բ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+2x+3��y�ύ�ڵ�C����D��0��1������P���������ϵĶ��㣮����PCD����CDΪ�ĵ��������Σ����P������Ϊ �� 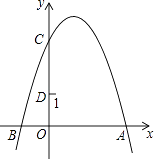
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ĵ�λ����Ϊ1��
��1�������A��D��ʾ������Ϊ�෴������ô��B��ʾ�����Ƕ��٣�
��2�������B��D��ʾ������Ϊ�෴������ôͼ�б�ʾ���ĸ����У���һ���ʾ�����ľ���ֵ���Ϊʲô��
��3������BΪԭ��ʱ��������һ��M��A�ľ����ǵ�M��D�ľ����2�������M����ʾ�������� ����
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����A�س�����B�����ߣ�ͬʱС�ϴ�B�س�����A�����ߣ���ͼ��ʾ���ཻ�ڵ�P�������߶�l1��l2�ֱ��ʾС����С����B�صľ���y��km��������ʱ��x��h��֮��Ĺ�ϵ����С����С�����ߵ��ٶȷֱ��ǣ�������

A. 3km/h��4km/h B. 3km/h��3km/h
C. 4km/h��4km/h D. 4km/h��3km/h
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�AC��BD�ཻ�ڵ�O��E��OD���е㣬����AE���ӳ���DC�ڵ�F����DF��FC=�� �� 
A.1��4
B.1��3
C.1��2
D.1��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ģ�ͼ1��һ����Ϊ2a����Ϊ2b�ij����Σ���ͼ���������ֳ��Ŀ�С�����Σ�Ȼ��ͼ2����״ƴ��һ��������.


![]() ͼ2����Ӱ���ֵ������εı߳���______.
ͼ2����Ӱ���ֵ������εı߳���______.
![]() �����ֲ�ͬ�ķ�����ͼ����Ӱ���ֵ����.
�����ֲ�ͬ�ķ�����ͼ����Ӱ���ֵ����.
������1��![]() = ____________��
= ____________��
������2��![]() = ____________��
= ____________��
(3) �۲�ͼ2��д��(a+b)2,(a-b)2,ab����������ʽ֮��ĵ�����ϵ��
![]() ����
����![]() ���еĵ�����ϵ��������⣺��m+n=10,m-n=6����mn��ֵ.
���еĵ�����ϵ��������⣺��m+n=10,m-n=6����mn��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com