
����Ŀ�������ڡ����ҹ��Ĵ�ͳ�ѽڣ���������гԡ���Բ����ϰ�ף�ijʳƷ��Ϊ�˽������ȥ�������Ϻõ����ڣ�A������ɳ�� ��B�������ڣ�C���������� ��D�����ֲ�ͬ��ζ��Բ��ϲ��������ڽ�ǰ��ij��������������˳������飬��������������Ƴ���������ͳ��ͼ���в��������������������Ϣ�ش�
��1�����βμӳ�������ľ����������� ���ˣ�
��2����ͼ �٢������������� ֱ�Ӳ�����ͼ�У�
��3����ͼ���б�ʾ��A����Բ�ĽǵĶ�����
��4������������8000�ˣ�����ư���D��Բ��������
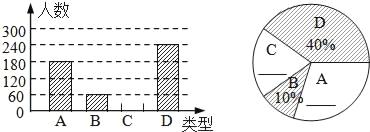
���𰸡���1��600����2��120�ˣ�20%��30%����3��108�㣨4������D��Բ������ԼΪ3200��
�����������������
��1��������ͳ��ͼ�е���Ϣ��֪��ϲ��B�����60�ˣ�ռ������������10%���ɴ˼��ɼ�����������������Ϊ60��10%=600���ˣ���
��2���ɣ�1�������ñ�����������Ϊ600�˽��ͳ��ͼ�����е����ݿɵ�ϲ��C�������Ϊ��600-180-60-240=120���ˣ���ϲ��C���ռ�������İٷֱ�Ϊ��120��600��100%=20%��ϲ��A���ռ�������İٷֱ�Ϊ��180��600��100%=30%���ɴ˼��ɽ�ͳ��ͼ����������
��3���ɣ�2�����������ݿɵ�����ͳ��ͼ��A������Ӧ��Բ�ĽǶ���Ϊ��360���30%=108�㣻
��4��������ͳ��ͼ�е���Ϣ��ϲ��D���ռ��������40%�ɵã�8000��40%=3200���ˣ���
���������
��1�����βμӳ�������ľ���������ǣ�60��10%=600���ˣ���
�ʴ�Ϊ��600��
��2��������ã�C������Ϊ600����180+60+240��=600��480=120���ˣ���C�İٷֱ�Ϊ120��600��100%=20%��A�İٷֱ�Ϊ180��600��100%=30%��
������ͳ��ͼ��������������ʾ��

��3����������ã�360���30%=108����
��ͼ���б�ʾ��A����Բ�ĽǵĶ���108����
��4��8000��40%=3200���ˣ���
������D��Բ������ԼΪ3200�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���������֣�������⣺���֪��![]() ������������������������ѭ��С�������
������������������������ѭ��С�������![]() ��С���������Dz�����ȫ����д����������С����
��С���������Dz�����ȫ����д����������С����![]() ��1����ʾ
��1����ʾ![]() ��С�����֣���Ϊ
��С�����֣���Ϊ![]() ������������1�����������ȥ���������֣������С�����֣�����
������������1�����������ȥ���������֣������С�����֣�����
��1��![]() �������������� �������������� ����
�������������� �������������� ����
��2�����![]() ��С������Ϊa��
��С������Ϊa��![]() ����������Ϊb����a+b��
����������Ϊb����a+b��![]() ��ֵ��
��ֵ��
��3����֪��10+![]() =x+y������x����������0��y��1����x��y���෴����
=x+y������x����������0��y��1����x��y���෴����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ɶ������ض��������֤����������������в�ͬ�����е��������������С������У�����ϲ�ķ��֣�������ȫ�ȵ�ֱ����������ͼ1��ͼ2�ڷ�ʱ���������������������֤����������С������ͼ1֤�����ɶ����Ĺ��̣�
������ȫ�ȵ�ֱ�������ΰ�ͼ1��ʾ�ڷţ�������DAB=90������֤��a2+b2=c2.
֤��������DB������D��BC���ϵĸ�DF����DF=EC=b��a��
��S�ı���ADCB=S��ACD+S��ABC= 12 b2+ 12 ab��
����S�ı���ADCB=S��ADB+S��DCB= 12 c2+ 12 a��b��a��
�� 12 b2+ 12 ab= 12 c2+ 12 a��b��a��
��a2+b2=c2
���������֤��������ͼ2��������֤����
������ȫ�ȵ�ֱ�������ΰ�ͼ2��ʾ�ڷţ�������DAB=90������֤��a2+b2=c2 ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���E��F�ֱ��ڱ�DC��AB�ϣ�DE=BF����ƽ���ı�����ֱ��EF�۵���ʹ�õ�B��C�ֱ�����B����C�������߶�EC�����߶�AF���ڵ�G������DG��B��G��
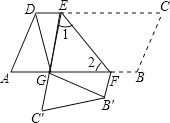
��֤����1����1=��2��
��2��DG=B��G��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��EΪCD���е㣬����AE��BE��BE��AE���ӳ�AE��BC���ӳ����ڵ�F��
��֤����1��FC��AD��
��2��AB��BC��AD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BD��AC��EF��AC��D��F�ֱ��Ǵ��㣬�ҡ�1����4����˵������ADG=��C.
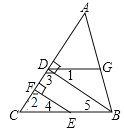
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
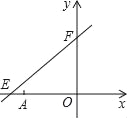
����Ŀ����ͼ��ֱ��y=![]() x+6��x�ᡢy��ֱ��ཻ�ڵ�E��F����A������Ϊ����6��0����P��x��y����ֱ��y=
x+6��x�ᡢy��ֱ��ཻ�ڵ�E��F����A������Ϊ����6��0����P��x��y����ֱ��y=![]() x+6��һ�����㣮
x+6��һ�����㣮
��1���ڵ�P�˶������У���д����OPA�����s��x�ĺ�����ϵʽ��
��2����P�˶���ʲôλ�ã���OPA�����Ϊ![]() �������ʱ��P�����ꣻ
�������ʱ��P�����ꣻ
��3����P��EF�Ĵ��߷ֱ�x�ᡢy����C��D���Ƿ���������ĵ�P��ʹ��COD�ա�FOE�������ڣ�ֱ��д����ʱ��P�����꣨��Ҫ��д�����̣����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����D�ڡ�O��ֱ��AB���ӳ����ϣ���C�ڡ�O�ϣ�AC=CD����ACD=120�㣮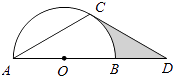
��1����֤��CD�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ2����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
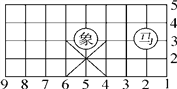
����Ŀ����ͼ���й��������̵�һ���֣������С��������ڵ�λ����(2��3)��ʾ��
(1)ͼ�С���λ�ÿɱ�ʾΪ____________��
(2)������������ӹ�������ֻ�ܴӡ��ա��ֵ�һ���ߵ�������Ե���һ�ǣ�����ֻ�ܴӡ���ֵ�һ���ߵ�������Ե���һ�ǣ��밴�˹���ֱ�д���������͡�����һ�����Ե����λ�ã�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com