【题目】如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．

求证：（1）FC＝AD；

（2）AB＝BC＋AD．

参考答案：

【答案】（1）证明见解析；（2）证明见解析.

【解析】试题分析:（1）根据AD∥BC可知∠ADC=∠ECF，再根据E是CD的中点可求出△ADE≌△FCE，根据全等三角形的性质即可解答．

（2）根据线段垂直平分线的性质判断出AB=BF即可．

证明：（1）∵AD∥BC（已知），

∴∠ADC=∠ECF（两直线平行，内错角相等），

∵E是CD的中点（已知），

∴DE=EC（中点的定义）．

∵在△ADE与△FCE中，

，

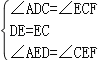∴△ADE≌△FCE（ASA），

∴FC=AD（全等三角形的性质）．

（2）∵△ADE≌△FCE，

∴AE=EF，AD=CF（全等三角形的对应边相等），

∴BE是线段AF的垂直平分线，

∴AB=BF=BC+CF，

∵AD=CF（已证），

∴AB=BC+AD（等量代换）．

关闭