
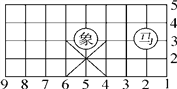
【题目】如图是中国象棋棋盘的一部分,棋盘中“马”所在的位置用(2,3)表示.
(1)图中“象”的位置可表示为____________;
(2)根据象棋的走子规则,“马”只能从“日”字的一角走到与它相对的另一角;“象”只能从“田”字的一角走到与它相对的另一角.请按此规则分别写出“马”和“象”下一步可以到达的位置.
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
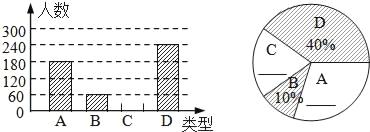
【题目】“春节”是我国的传统佳节,民间历来有吃“汤圆”的习俗.某食品厂为了解市民对去年销量较好的肉馅(A)、豆沙馅 (B)、菜馅(C)、三丁馅 (D)四种不同口味汤圆的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).请根据以上信息回答:
(1)本次参加抽样调查的居民人数是 人;
(2)将图 ①②补充完整;( 直接补填在图中)
(3)求图②中表示“A”的圆心角的度数;
(4)若居民区有8000人,请估计爱吃D汤圆的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF:FC=( ) 
A.1:4
B.1:3
C.1:2
D.1:1
查看答案和解析>>
科目:初中数学 来源: 题型:
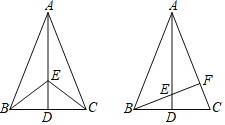
【题目】在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE.
(2)如图,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45,原题设其它条件不变,求证:△AEF≌△BCF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知:AB∥CD,点E,F分别在AB,CD上,且OE⊥OF.
(1)求证:∠1+∠2=90°;
(2)如图2,分别在OE,CD上取点G,H,使FO平分∠CFG,EO平分∠AEH,求证:FG∥EH.
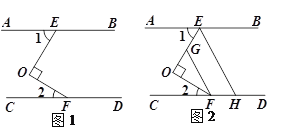
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F. 
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)图1是一个长为2a,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按图2的形状拼成一个正方形.


![]() 图2的阴影部分的正方形的边长是______.
图2的阴影部分的正方形的边长是______.
![]() 用两种不同的方法求图中阴影部分的面积.
用两种不同的方法求图中阴影部分的面积.
(方法1)![]() = ____________;
= ____________;
(方法2)![]() = ____________;
= ____________;
(3) 观察图2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系;
![]() 根据
根据![]() 题中的等量关系,解决问题:若m+n=10,m-n=6,求mn的值.
题中的等量关系,解决问题:若m+n=10,m-n=6,求mn的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“世界杯”期间,某娱乐场所举办“消夏看球赛”活动,需要对会场进行布置,计划在现场安装小彩灯和大彩灯.已知安装5个小彩灯和4个大彩灯共需150元;安装7个小彩灯和6个大彩灯共需220元.
(1)安装1个小彩灯和1个大彩灯各需多少元?
(2)若场地共需安装小彩灯和大彩灯300个,费用不超过4350元,则最多安装大彩灯多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个形如六边形的点阵,它的中心是一个点,算做第一层,第二层每边两个点,第三层每边三个点,以此类推.

(1)填写下表
层数 | 1 | 2 | 3 | 4 | 5 |
该层对应的点数 | 1 | 6 | 12 |
(2)写出第n层对应的点数(n≥2);
(3)如果某层一共有72个点,请你求出对应的层数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com