
【题目】(题文)图1是一个长为2a,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按图2的形状拼成一个正方形.


![]() 图2的阴影部分的正方形的边长是______.
图2的阴影部分的正方形的边长是______.
![]() 用两种不同的方法求图中阴影部分的面积.
用两种不同的方法求图中阴影部分的面积.
(方法1)![]() = ____________;
= ____________;
(方法2)![]() = ____________;
= ____________;
(3) 观察图2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系;
![]() 根据
根据![]() 题中的等量关系,解决问题:若m+n=10,m-n=6,求mn的值.
题中的等量关系,解决问题:若m+n=10,m-n=6,求mn的值.
【答案】a-b(a-b)2(a+b)2-4ab
【解析】
(1)观察图形的特征可得结果;(2)可分别利用边长的平方和大正方形的面积减去小正方形的面积两种方法得到中间小正方形的面积;(3)根据两幅图的空白处面积相等即可得到它们之间的关系.(4)根据(3)中的结论直接整体代入即可求出mn的值.
的1)式或地次因式人方相等,数写厉线的定底色
(1)a-b;
(2)方法1:S阴影=(a-b)2,
方法2:S阴影=(a+b)2-4ab;
(3)(a+b)2,(a-b)2,ab这三个代数式之间的等量关系为:(a-b)2=(a+b)2-4ab;![]() 根据
根据![]() 题中的结论得(m-n)2=(m+n)2-4mn,
题中的结论得(m-n)2=(m+n)2-4mn,
∵ m+n=10,m-n=6,
∴ 36=100-4mn,
∴ mn=16.


科目:初中数学 来源: 题型:
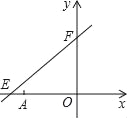
【题目】如图,直线y=![]() x+6与x轴、y轴分别相交于点E、F,点A的坐标为(﹣6,0),P(x,y)是直线y=
x+6与x轴、y轴分别相交于点E、F,点A的坐标为(﹣6,0),P(x,y)是直线y=![]() x+6上一个动点.
x+6上一个动点.
(1)在点P运动过程中,试写出△OPA的面积s与x的函数关系式;
(2)当P运动到什么位置,△OPA的面积为![]() ,求出此时点P的坐标;
,求出此时点P的坐标;
(3)过P作EF的垂线分别交x轴、y轴于C、D.是否存在这样的点P,使△COD≌△FOE?若存在,直接写出此时点P的坐标(不要求写解答过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,DC⊥BC,AE 平分∠BAD,DE 平分∠ADC,以下结论:①∠AED=90°;②点 E 是 BC 的中点;③DE=BE;④AD=AB+CD;其中正确的是( )
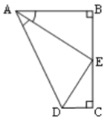
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
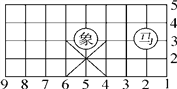
【题目】如图是中国象棋棋盘的一部分,棋盘中“马”所在的位置用(2,3)表示.
(1)图中“象”的位置可表示为____________;
(2)根据象棋的走子规则,“马”只能从“日”字的一角走到与它相对的另一角;“象”只能从“田”字的一角走到与它相对的另一角.请按此规则分别写出“马”和“象”下一步可以到达的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图一次函数y= ![]() x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=
x+1的图象与x轴交于点A,与y轴交于点B;二次函数y= ![]() x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y= ![]() x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0).
x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0).
(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( ) 
A.40°
B.60°
C.70°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移 ![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老王的房子准备开始装修,请来师徒二人做泥水.已知师傅单独完成需10天,徒弟单独完成需15天。
(1)若两人先合作2天,剩下的由徒弟单独做,结果超出老王预期的工期3天完成,求老王预期的工期天数;
(2)若师傅的工价每天300元,徒弟的工价每天220元,老王房子的泥水工价预算不超过3180元,问师傅至少要做几天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com