
【题目】如图,AC,BD相交于点O,AC平分∠DCB,CD⊥AD,∠ACD=45°,∠BAC=60°.
(1)证明:AD∥BC;
(2)求∠EAD的度数;
(3)求证:∠AOB=∠DAC +∠CBD

【答案】(1)见解析;(2)75°;(3)见解析.
【解析】(1)由AC平分∠DCB,∠ACD=45°,可得∠BCD=90°,从而可证AD∥BC;
(2)由AD∥BC可求∠ACB=∠ACD=45°,然后由三角形内角和可求出∠ABC的度数,再根据两直线平行,同位角相等可求出∠EAD的度数;;
(3)过点O作OF∥AD,则OF∥BC,根据平行线的性质可得∠AOF=∠DAC,∠FOB=∠CBD,然后等量代换可得结论.
⑴ 证明:∵AC平分∠DCB,
∴∠BCD=2∠ACD=2×45°=90°.
∵CD⊥AD,
∴∠ADC=90°,
∴∠BCD+∠ADC=90°+90°=180°,
∴AD∥BC;
⑵ ∵AC平分∠DCB,
∴∠ACB=∠ACD=45°,
∵AD∥BC,
∴∠DAC=∠ACB=45°,
∴∠EAD=180°-∠DAC-∠BAC
=180°-45°-60°
=75°;
⑶ 过点O作OF∥AD,
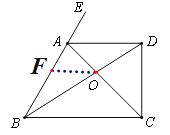
∵AD∥BC,
∴OF∥BC,
∴∠AOF=∠DAC,∠FOB=∠CBD,
∴∠AOB=∠AOF+∠FOB=∠DAC+∠CBD.


科目:初中数学 来源: 题型:
【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.根据两人的作法可判断( )

A. 甲正确,乙错误 B. 乙正确,甲错误
C. 甲、乙均正确 D. 甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是 ( )

A. A1(4,4),C1(3,2) B. A1(3,3),C1(2,1)
C. A1(4,3),C1(2,3) D. A1(3,4),C1(2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
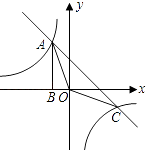
【题目】如图,Rt△ABO的顶点A是双曲线y1= ![]() 与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO= ![]() .
. 
(1)求这两个函数的解析式;
(2)求△AOC的面积;
(3)直接写出使y1>y2成立的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,下列结论正确的有( )
①AD=BD=BC;②△BCD≌△ABC;③AD2=ACDC;④点D是AC的黄金分割点.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图所示,AB//CD,点E在AD的延长线上,∠EDC与∠B互为补角.
(1)问AD,BC是否平行?请说明理由;
(2)如果∠EDC=72°,∠1=∠2=2∠CAB,求∠CAF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民公园划出一块矩形区域,用以栽植鲜花.
(1)经测量,该矩形区域的周长是72m,面积为320m2 , 请求出该区域的长与宽;
(2)公园管理处曾设想使矩形的周长和面积分别为(1)中区域的周长和面积的一半,你认为此设想合理吗?如果此设想合理,请求出其长和宽;如果不合理,请说明理由,并求出在(1)中周长减半的条件下矩形面积的最大值. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的速度分别是( )

A. 3km/h和4km/h B. 3km/h和3km/h
C. 4km/h和4km/h D. 4km/h和3km/h
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com