
����Ŀ���Ķ����ϣ���ش���������
����һ���ҹ��Ŵ���ѧ���ؾ����ڡ�������¡��м���������б�������������֪�����ε����߳�����������������ִ�ʽ�ӱ�ʾ��Ϊ��S��![]() ���٣�����a��b��cΪ�����ε����߳���SΪ���������һ�������Ź���ϣ��Ҳ���������������������ʽ����S��
���٣�����a��b��cΪ�����ε����߳���SΪ���������һ�������Ź���ϣ��Ҳ���������������������ʽ����S��![]() �����ڣ�����p��
�����ڣ�����p��![]() ��
��
���϶�������ƽ���ʽ��a2��b2����a+b����a��b��
��ʽ���ÿɵã���a+b����a��b����a2��b2��
����a2����b+c��2����a+b+c����a��b��c��
��1������֪�����ε����߳��ֱ�Ϊ3��4��5�����Էֱ����ù�ʽ�ٺ�ʽ�ڣ�����������ε������
��2�����ܷ��ɹ�ʽ���Ƶ�����ʽ�ڣ������ԣ�
���𰸡���1�������ε����Ϊ6����2��������.
��������
��1�����ݲ��ϣ����빫ʽ������⣻
��2������ƽ���ʽ����ȫƽ����ʽ�����Ƶ���
�⣺��1����a��3��b��4��c��5��
��32+42��25��52��25��
��a2+b2��c2��
a2b2��144��
��S��![]() ��
��![]() ��6��
��6��
��p��![]() ��
��![]() ��6��
��6��
p��a��6��3��3��p��b��6��4��2��p��c��6��5��1��
S��![]()
��![]()
��6��
�������ε����Ϊ6��
��2����![]() [a2b2����
[a2b2����![]() ��2]
��2]
��![]() [
[![]() ��
��![]() ]
]
��![]() [��a+b��2��c2][c2����a��b��2]
[��a+b��2��c2][c2����a��b��2]
��![]() ��a+b+c����a+b��c����a+c��b����b+c��a��
��a+b+c����a+b��c����a+c��b����b+c��a��
��![]() ��2p��2p��2c����2p��2b����2p��2a��
��2p��2p��2c����2p��2b����2p��2a��
��p��p��a����p��b����p��c��
��![]() ��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Լ�����Խ����ഹֱ���ı��ν����������Ρ���
��1�����ڡ�ƽ���ı��Σ����Σ����Σ������Ρ��У�һ���ǡ������Ρ������� ����
�����ı���ABCD�У�AB=AD��CB��CD������ı����� ���������Ρ�������ǡ����ǡ���
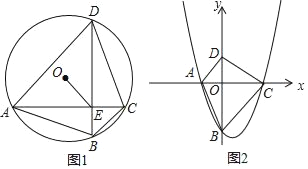
��2����ͼ1��A��B��C��D�ǰ뾶Ϊ1�ġ�O�ϰ���ʱ�뷽�����е��ĸ����㣬AC��BD���ڵ�E����ACB����CDB=��ACD����CBD����![]() ��OE��
��OE��![]() ʱ����AC2+BD2��ȡֵ��Χ��
ʱ����AC2+BD2��ȡֵ��Χ��
��3����ͼ2����ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c��a��b��cΪ������a��0��c��0����x�ύ��A��C���㣨��A�ڵ�C����ࣩ��B����������y��Ľ��㣬��D������Ϊ��0����ac�����ǡ������Ρ�ABCD�����ΪS���ǡ�AOB����COD����AOD����BOC������ֱ�ΪS1��S2��S3��S4����ֱ��д�������������������������ߵĽ���ʽ��
��![]() �� ��
�� ��![]() �� �ۡ������Ρ�ABCD���ܳ�Ϊ12
�� �ۡ������Ρ�ABCD���ܳ�Ϊ12![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
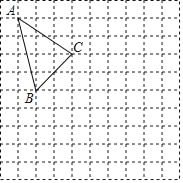
����Ŀ����ͼ���������������У�ÿ��С�����εı߳�Ϊ1�������ABC�������������ߵĽ����ϣ��Ķ���A��C������ֱ�ΪA����3��4��C��0��2��
��1�������������ڵ�ƽ���ڽ���ƽ��ֱ������ϵ����д����B�����ꣻ
��2��������ABC����ԭ��ԳƵ�ͼ����A1B1C1��
��3������ABC�������
��4����x���ϴ���һ��P��ʹPA+PB��ֵ��С����ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAD=��CAE=90�㣬AB=AD��AE=AC��AF��CB������ΪF��
��1����֤����ABC�ա�ADE��
��2������FAE�Ķ�����
��3����֤��CD=2BF+DE��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ڼ䣬ij��λ8���쵼��320��Ա�������������������չ���������45����30��С����������2����3��С���������1700Ԫ��������3����2��С���������1800Ԫ
��1�����С��ÿ������Ѹ��Ƕ���Ԫ��
��2����ÿ����������Ҫ��һ���쵼��ÿ���˾�����λ����������ò�����3100Ԫ������ʡǮ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����ij��Ʒ�Ƶ��ֻ�,ÿ��������Ϊ2500Ԫ.�г����б����������ۼ�Ϊ2900Ԫʱ,ƽ��ÿ�����۳�8�����������ۼ�ÿ����50Ԫʱ,ƽ��ÿ����ܶ��۳�4��.
��1�����ۼ�Ϊ2800Ԫʱ,�����ֻ�ƽ��ÿ�����������ﵽ����Ԫ?
��2������ÿ���ֻ�����xԪ,ÿ�����������ΪyԪ,��д��y��x֮��ĺ�����ϵʽ��
��3���̳�Ҫ�����������,ÿ���ֻ����ۼ�Ӧ��ΪΪ����Ԫ����ʱ����������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���P��CD���е㣬��BCD=60��������AP��BC���ӳ����ڵ�E������BP��DE�ڵ�K����O���߶�BK���е㣮
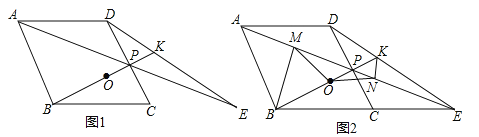
��1����֤����ADP�ա�ECP��
��2����BP=nPK�������n��ֵ��
��3����BM�AAE�ڵ�M����KN�AAE�ڵ�N������MO��NO����ͼ2��ʾ����֤����MON�ǵ��������Σ���ֱ��д����MON�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵxoy�У���M��x����������ϣ���M��x����A��B���㣬��y����C��D���㣬��CΪ��AE���е㣬AE��y����G�㣬����A������Ϊ��-1��0����AE=4
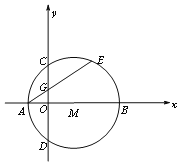
��1�����C�����ꣻ
��2������MG��BC����֤��MG��BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������������ȫ��ͬ������С�����Ϸֱ�������֣�1��1��2.�������һ��С��(���Ż�)�������ּ�Ϊp�������������һ��С�������ּ�Ϊq����p��qʹ����x�ķ���x2��px��q��0��ʵ�����ĸ�����(����)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com