
ЁОЬтФПЁПФГЩЬГЁЯњЪлФГжжЦЗХЦЕФЪжЛњ,УПВПНјЛѕМлЮЊ2500дЊ.ЪаГЁЕїбаБэУїЃКЕБЯњЪлМлЮЊ2900дЊЪБ,ЦНОљУПЬьФмЪлГі8ВПЃЛЖјЕБЯњЪлМлУПНЕЕЭ50дЊЪБ,ЦНОљУПЬьОЭФмЖрЪлГі4ВП.
ЃЈ1ЃЉЕБЪлМлЮЊ2800дЊЪБ,етжжЪжЛњЦНОљУПЬьЕФЯњЪлРћШѓДяЕНЖрЩйдЊ?
ЃЈ2ЃЉШєЩшУПВПЪжЛњНЕЕЭxдЊ,УПЬьЕФЯњЪлРћШѓЮЊyдЊ,ЪдаДГіyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ3ЃЉЩЬГЁвЊЯыЛёЕУзюДѓРћШѓ,УПВПЪжЛњЕФЪлМлгІЖЉЮЊЮЊЖрЩйдЊЃПДЫЪБЕФзюДѓРћШѓЪЧЖрЩйдЊЃП
ЁОД№АИЁПЃЈ1ЃЉЕБЪлМлЮЊ2800дЊЪБ,етжжЪжЛњЦНОљУПЬьЕФЯњЪлРћШѓДяЕН4800дЊЃЛ
ЃЈ2ЃЉ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉУПЬЈВЪЕчНЕМл150дЊЪБ,ЩЬГЁУПЬьЯњЪлетжжВЪЕчЕФРћШѓзюДѓ,зюДѓРћШѓЪЧ5000дЊЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉЕБЪлМлЮЊ2800дЊЪБ,ЯњЪлМлНЕЕЭ100дЊ,ЦНОљУПЬьОЭФмЪлГі16ВП.МДПЩЧѓГіУПЬьРћШѓЃЛ
ЃЈ2ЃЉИљОнЃКРћШѓ=ЃЈУПЬЈЪЕМЪЪлМлЉУПЬЈНјМлЃЉЁСЯњЪлСП,УПЬЈЪЕМЪЪлМл=2900Љx,ЯњЪлСП=8+4ЁС![]() ,СаКЏЪ§ЙиЯЕЪНЃЛ
,СаКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉРћгУЖўДЮКЏЪ§ЕФЖЅЕузјБъЙЋЪН,ЧѓКЏЪ§ЕФзюДѓжЕЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЕБЪлМлЮЊ2800дЊЪБ,ЯњЪлМлНЕЕЭ100дЊ,ЦНОљУПЬьОЭФмЪлГі16ВП.
ЫљвдЃКетжжЪжЛњЦНОљУПЬьЕФЯњЪлРћШѓЮЊЃК![]() ЃЈдЊЃЉЃЛ
ЃЈдЊЃЉЃЛ
ЃЈ2ЃЉИљОнЬтвт,ЕУ![]() ,
,
МД![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЖдгк![]() ,
,
ЕБ![]() ЪБ,
ЪБ,
![]()
Ыљвд,УПЬЈВЪЕчНЕМл150дЊЪБ,ЩЬГЁУПЬьЯњЪлетжжВЪЕчЕФРћШѓзюДѓ,зюДѓРћШѓЪЧ5000дЊЃЎ


 ЬиИпМЖНЬЪІЕуВІЯЕСаД№АИ
ЬиИпМЖНЬЪІЕуВІЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() КЭ
КЭ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌе§ЗНаЮ
ЃЌе§ЗНаЮ![]() ЕФБп
ЕФБп![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() .
.
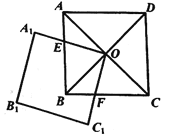
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЙће§ЗНаЮ![]() ЕФБпГЄЮЊ
ЕФБпГЄЮЊ![]() ЃЌФЧУДе§ЗНаЮ
ЃЌФЧУДе§ЗНаЮ![]() ШЦ
ШЦ![]() ЕузЊЖЏЕФЙ§ГЬжаЃЌгые§ЗНаЮ
ЕузЊЖЏЕФЙ§ГЬжаЃЌгые§ЗНаЮ![]() жиЕўВПЗжЕФУцЛ§ЪМжеЕШгк__________.ЃЈгУКЌ
жиЕўВПЗжЕФУцЛ§ЪМжеЕШгк__________.ЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉ
ЕФДњЪ§ЪНБэЪОЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
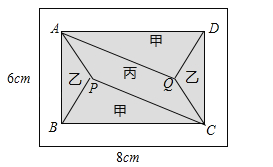
ЁОЬтФПЁПЃЈ2017еуНЪЁЮТжнЪаЃЉаЁЛЦзМБИИјГЄ8mЃЌПэ6mЕФГЄЗНаЮПЭЬќЦЬЩшДЩзЉЃЌЯжНЋЦфЛЎЗжГЩвЛИіГЄЗНаЮABCDЧјгђЂёЃЈвѕгАВПЗжЃЉКЭвЛИіЛЗаЮЧјгђЂђЃЈПеАзВПЗжЃЉЃЌЦфжаЧјгђЂёгУМзЁЂввЁЂБћШ§жжДЩзЉЦЬЩшЃЌЧвТњзуPQЁЮADЃЌШчЭМЫљЪОЃЎ
ЃЈ1ЃЉШєЧјгђЂёЕФШ§жжДЩзЉОљМлЮЊ300дЊ/m2ЃЌУцЛ§ЮЊSЃЈm2ЃЉЃЌЧјгђЂђЕФДЩзЉОљМлЮЊ200дЊ/m2ЃЌЧвСНЧјгђЕФДЩзЉзмМлЮЊВЛГЌЙ§12000дЊЃЌЧѓSЕФзюДѓжЕЃЛ
ЃЈ2ЃЉШєЧјгђЂёТњзуBC=2ЃК3ЃЌЧјгђЂђЫФжмПэЖШЯрЕШЃЎ
ЂйЧѓABЃЌBCЕФГЄЃЛ
ЂкШєМзЁЂБћСНДЩзЉЕЅМлжЎКЭЮЊ300дЊ/m2ЃЌввЁЂБћДЩзЉЕЅМлжЎБШЮЊ5ЃК3ЃЌЧвЧјгђЂёЕФШ§жжДЩзЉзмМлЮЊ4800дЊЃЌЧѓБћДЩзЉЕЅМлЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
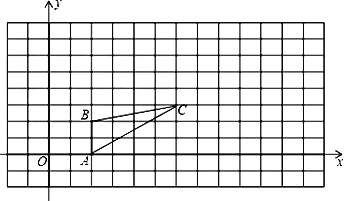
ЁОЬтФПЁПШчЭМЃЌЭМжаЕФаЁЗНИёЖМЪЧБпГЄЮЊ1ЕФе§ЗНаЮЃЌЁїABCЕФAЁЂBЁЂCШ§ЕузјБъЮЊAЃЈ2,0ЃЉЁЂBЃЈ2,2ЃЉЁЂCЃЈ6ЃЌ3ЃЉЁЃ
ЃЈ1ЃЉ ЧыдкЭМжаЛГівЛИіЁї![]() ,ЪЙЁї
,ЪЙЁї![]() гыЁїABCЪЧвдзјБъдЕуЮЊЮЛЫЦжааФЃЌЯрЫЦБШЮЊ2ЕФЮЛЫЦЭМаЮЁЃ
гыЁїABCЪЧвдзјБъдЕуЮЊЮЛЫЦжааФЃЌЯрЫЦБШЮЊ2ЕФЮЛЫЦЭМаЮЁЃ
ЃЈ2ЃЉЧѓЁї![]() ЕФУцЛ§ЁЃ
ЕФУцЛ§ЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвде§ЗНаЮЕФжааФOЮЊЖЅЕузївЛИіжБНЧЃЌжБНЧЕФСНБпЗжБ№НЛе§ЗНаЮЕФСНБпBCЁЂDCгкEЁЂFЕуЃЌЮЪЃК
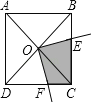
ЃЈ1ЃЉЁїBOEгыЁїCOFгаЪВУДЙиЯЕЃПжЄУїФуЕФНсТлЃЈЬсЪОЃКе§ЗНаЮЕФЖдНЧЯпАбе§ЗНаЮЗжГЩШЋЕШЕФЫФИіЕШбќжБНЧШ§НЧаЮЃЌМДе§ЗНаЮЕФЖдНЧЯпДЙжБЯрЕШЧвЯрЛЅЦНЗжЃЉЃЛ
ЃЈ2ЃЉШєе§ЗНаЮЕФБпГЄЮЊ2ЃЌЫФБпаЮEOFCЕФУцЛ§ЮЊЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
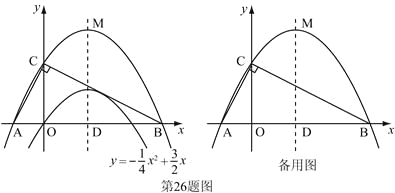
ЁОЬтФПЁПЃЈБОЬтТњЗж12ЗжЃЉвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓШчЭМ.
ЕФЭМЯѓШчЭМ.
ЃЈ1ЃЉЧѓЫќЕФЖдГЦжсгы![]() жсНЛЕуDЕФзјБъЃЛ
жсНЛЕуDЕФзјБъЃЛ
ЃЈ2ЃЉНЋИУХзЮяЯпбиЫќЕФЖдГЦжсЯђЩЯЦНвЦЃЌЩшЦНвЦКѓЕФХзЮяЯпгы![]() жсЃЌ
жсЃЌ![]() жсЕФНЛЕуЗжБ№ЮЊAЁЂBЁЂCШ§ЕуЃЌШєЁЯACB=90ЁуЃЌЧѓДЫЪБХзЮяЯпЕФНтЮіЪНЃЛ
жсЕФНЛЕуЗжБ№ЮЊAЁЂBЁЂCШ§ЕуЃЌШєЁЯACB=90ЁуЃЌЧѓДЫЪБХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЩшЃЈ2ЃЉжаЦНвЦКѓЕФХзЮяЯпЕФЖЅЕуЮЊMЃЌвдABЮЊжБОЖЃЌDЮЊдВаФзїЁбDЃЌЪдХаЖЯжБЯпCMгыЁбDЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ЪЧЕзБп
ЪЧЕзБп![]() ЕФжаЕуЃЌСНБпЗжБ№гы
ЕФжаЕуЃЌСНБпЗжБ№гы![]() НЛгкЕу
НЛгкЕу![]() ЃЎ
ЃЎ
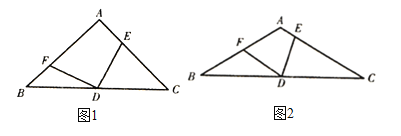
ЃЈ1ЃЉШчЭМ1ЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() ЕФЮЛжУБфЛЏЪБЃЌ
ЕФЮЛжУБфЛЏЪБЃЌ![]() ЪЧЗёЫцжЎБфЛЏЃПжЄУїФуЕФНсТлЃЛ
ЪЧЗёЫцжЎБфЛЏЃПжЄУїФуЕФНсТлЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБ![]() ЃЌЕБ
ЃЌЕБ![]() ЁуЪБЃЌЃЈ1ЃЉжаЕФНсТлШдШЛГЩСЂЃЌЧѓГіДЫЪБ
ЁуЪБЃЌЃЈ1ЃЉжаЕФНсТлШдШЛГЩСЂЃЌЧѓГіДЫЪБ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкЁїABCжа,AB=AC=13,BC=10,ЕуDЮЊBCЕФжаЕу,DEЁЭABгкЕуE,дђtan ЁЯBDE=

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
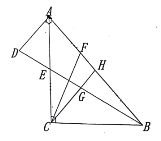
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЙ§Еу
ЕФжаЕуЃЌЙ§Еу![]() зї
зї![]() ДЙжБ
ДЙжБ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЎ
ЃЎ![]() ЮЊ
ЮЊ![]() жаЕуЃЌ
жаЕуЃЌ![]() НЛ
НЛ![]() гк
гк![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() БпЩЯвЛЕуЃЌСЌНг
БпЩЯвЛЕуЃЌСЌНг![]() ЃЌЧв
ЃЌЧв![]() ЃЎ
ЃЎ
(1)Шє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЖШЃЛ
ЕФГЄЖШЃЛ
(2)ЧѓжЄЃК![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com