
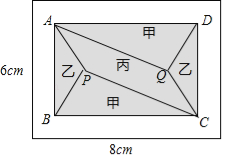
����Ŀ����2017�㽭ʡ�����У�С��������8m����6m�ij����ο��������ש���ֽ��仮�ֳ�һ��������ABCD�������Ӱ���֣���һ����������հײ��֣�������������üס��ҡ������ִ�ש���裬������PQ��AD����ͼ��ʾ��
��1�������������ִ�ש����Ϊ300Ԫ/m2�����ΪS��m2���������Ĵ�ש����Ϊ200Ԫ/m2����������Ĵ�ש�ܼ�Ϊ������12000Ԫ����S�����ֵ��
��2�������������BC=2��3����������ܿ�����ȣ�
����AB��BC�ij���
�����ס�������ש����֮��Ϊ300Ԫ/m2���ҡ�����ש����֮��Ϊ5��3�������������ִ�ש�ܼ�Ϊ4800Ԫ�������ש���۵�ȡֵ��Χ��
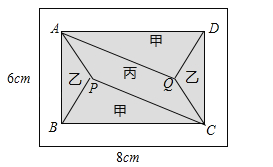
���𰸡���1��24����2����AB=4��CB=6���ڱ���ש����3x�ķ�ΧΪ150��3x��300Ԫ/m2��
�����������⣨1����������ɵ�300S+��48��S��200��12000���ⲻ��ʽ���ɣ�
��2���������������ܿ���Ϊa���������⣨6��2a������8��2a��=2��3�����a=1���ɴ˼��ɽ�����⣻
�����ҡ�����ש���۷ֱ�Ϊ5xԪ/m2��3xԪ/m2����ĵ���Ϊ��300��3x��Ԫ/m2����PQ��AD���ɵü����=����ABCD�������һ��=12�����ҵ����Ϊs����������Ϊ��12��s����������12��300��3x��+5xs+3x��12��s��=4800�����s=![]() ����0��s��12���ɵ�0��
����0��s��12���ɵ�0��![]() ��12���ⲻ��ʽ����
��12���ⲻ��ʽ����
�����������1��������300S+��48��S��200��12000��
���S��24��
��S�����ֵΪ24��
��2���������������ܿ���Ϊa���������⣨6��2a������8��2a��=2��3�����a=1��
��AB=6��2a=4��CB=8��2a=6��
�����ҡ�����ש���۷ֱ�Ϊ5xԪ/m2��3xԪ/m2����ĵ���Ϊ��300��3x��Ԫ/m2��
��PQ��AD��
�������=����ABCD�������һ��=12�����ҵ����Ϊs����������Ϊ��12��s����
������12��300��3x��+5xs+3x��12��s��=4800��
���s=![]() ��
��
��0��s��12��
��0��![]() ��12��
��12��
��0��x��50��
������ש����3x�ķ�ΧΪ0��3x��150Ԫ/m2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
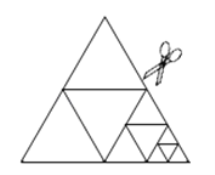
����Ŀ����ͼ����һ����������ֽƬ�����ĸ�С�������Σ��õ�![]() ��С�������Σ���Ϊ��һ�β���; Ȼ�����е�һ�����������ټ����ĸ�С�������Σ����õ�
��С�������Σ���Ϊ��һ�β���; Ȼ�����е�һ�����������ټ����ĸ�С�������Σ����õ�![]() ��С�������Σ���Ϊ�ڶ��β���;�ٽ����е�һ�����������ټ����ĸ�С�������Σ����õ�
��С�������Σ���Ϊ�ڶ��β���;�ٽ����е�һ�����������ټ����ĸ�С�������Σ����õ�![]() ��С�������Σ���Ϊ�����β����������������ϲ�������Ҫ�õ�
��С�������Σ���Ϊ�����β����������������ϲ�������Ҫ�õ�![]() ��С�������Σ�����Ҫ�����Ĵ�����__________�Σ�
��С�������Σ�����Ҫ�����Ĵ�����__________�Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���![]() ��ͼ����
��ͼ����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��һ�κ���
��һ�κ���![]() ��ͼ�����
��ͼ�����![]() ������
������![]() �ἰ
�ἰ![]() ��ͼ��ֱ��ڵ�
��ͼ��ֱ��ڵ�![]() ��
��![]() ��
��![]() ������Ϊ
������Ϊ![]() .
.
��1����n��ֵ��һ�κ���![]() �Ľ���ʽ.
�Ľ���ʽ.
��2�����ı���![]() �����.
�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵxOy�еĵ�P��a��b��������P��������Ϊ��a+kb��ka+b��������kΪ��������k��0����
��Ƶ�P��Ϊ��P����k���������������磺P��1��4������2����������ΪP�䣨1+2��4��2��1+4������P�䣨9��6����
��������P����2��3������3����������P���������� ����
����������P����5����������P��������Ϊ��3����9�������P�����ꣻ
����������P��x����������ϣ���P����k����������ΪP���㣬���߶�PP���ij���Ϊ�߶�OP���ȵ�2������k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����CAB=��DBA��������һ����������һ�����ж���ABC�ա�BAD���ǣ�������
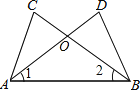
A. AC=BDB. ��1=��2C. AD=BCD. ��C=��D
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����Ȼ�������������Է��ѳ����ɸ����������ĺ͡����磺![]() ��
��![]() �ֱ������ͼ��ʾ�ķ�ʽ����������2����3����4�����������ĺͣ���
�ֱ������ͼ��ʾ�ķ�ʽ����������2����3����4�����������ĺͣ���![]() =3+5��
=3+5��![]() =7+9+11��
=7+9+11��![]() =13+15+17+19��������
=13+15+17+19��������![]() Ҳ���մ˹���������������������
Ҳ���մ˹���������������������![]() �����������������У�����������______.
����������������������������______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����O�ǵȱ�������ABC��һ�㣬��AOB=110������BOC=��, ��OCΪ�����ȱ�������OCD������AD.

��1������=150��ʱ�����ж���AOD����״����˵�����ɣ�
��2��̽������aΪ���ٶ�ʱ����AOD�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
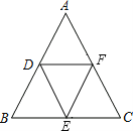
����Ŀ����ͼ������ABC�У���B=��C=��DEF����D��E��F�ֱ���AB��AC�ϣ���BD=CE����֤��DE=EF��
֤�������뽫�����֤�����̲���������
�ߡ�B+��BDE+��BED=180����______��
��DEF+��FEC+��BED=180����______��
��B=��DEF����֪��
���BDE=��FEC��______��
����BDE����CEF��
��B=��C����֪��
BD=CE��______��
��BDE=��FEC��______��
���BDE�ա�CEF��______��������ĸ��ʾ��
��DE=EF��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и����ֱ������������ڵļ��ϵ������ڣ�
9��![]() ��+4.3��|��0.5|����(+7)��18%��(��13)4����6��0��
��+4.3��|��0.5|����(+7)��18%��(��13)4����6��0��
����������{_________}
����������{_________}
����������{__________}
�Ǹ���������{________}��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com