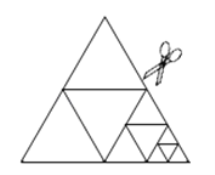
【题目】如图，将一张正三角形纸片剪成四个小正三角形，得到
个小正三角形，称为第一次操作; 然后，将其中的一个正三角形再剪成四个小正三角形，共得到
个小正三角形，称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形，共得到
个小正三角形，称为第三次操作；…，根据以上操作，若要得到
个小正三角形，则需要操作的次数是__________次．
通城学典默写能手系列答案科目：初中数学 来源： 题型：
【题目】如图，∠MBC和∠NCB是△ABC的外角，点O是∠MBC和∠NCB的平分线的交点，点O叫做△ABC的旁心.
(1)已知∠A＝100°，那么∠BOC等于多少度；
(2)猜想∠BOC与∠A有什么数量关系?并证明你的猜想.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在第23个世界读书日前夕，我市某中学为了解本校学生的每周课外阅读时间
用t表示，单位：小时
，采用随机抽样的方法进行问卷调查，调查结果按
，
，
，
分为四个等级，并依次用A，B，C，D表示，根据调查结果统计的数据，绘制成了如图所示的两幅不完整的统计图，由图中给出的信息解答下列问题：
求本次调查的学生人数；
求扇形统计图中等级B所在扇形的圆心角度数，并把条形统计图补充完整；
若该校共有学生1200人，试估计每周课外阅读时间满足的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一架直升机从高度为450米的位置开始，先以20米/秒的速度上升60秒，后以12米/秒的速度下降120秒，规定上升为正，下降为负，求：
（1）这时直升机的高度是多少米？
（2）直升机每上升1米耗油
毫升，每下降1米耗油
毫升（其中
），问这架直升机在上升和下降的过程中共耗油多少毫升？
（3）若
是小于
的最大整数，求（2）问中的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】关于x的方程ax2+bx+c=0（a
0）.
（1）已知a，c异号，试说明此方程根的情况.
（2）若该方程的根是x1=-1，x2=3，试求方程a（x+2）2+bx+2b+c=0的根.
查看答案和解析>>
科目：初中数学 来源： 题型：
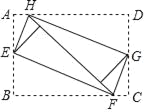
【题目】如图，将矩形ABCD的四个角向内折叠铺平，恰好拼成一个无缝隙无重叠的矩形EFGH，若EH＝5，EF＝12，则矩形ABCD的面积是（ ）
A. 13 B. 
C. 60 D. 120
查看答案和解析>>
科目：初中数学 来源： 题型：
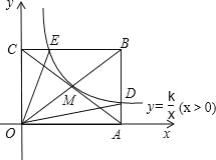
【题目】如图，反比例函数y＝
（x＞0）的图象经过矩形OABC对角线的交点M，分别交AB、BC于点D、E，连结DE．若四边形ODBE的面积为9，则△ODE的面积是________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义符号min{a，b}的含义为：当a≥b时min{a，b}=b；当a≤b时min{a，b}=a．如：min{1，-3}=﹣3，min{﹣4，﹣2}=﹣4，则min{﹣x2+2，﹣x}的最大值是（ ）
A. ﹣1 B. ﹣2 C. 1 D. 0
查看答案和解析>>
科目：初中数学 来源： 题型：
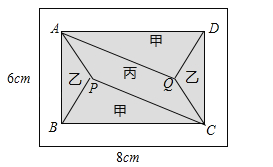
【题目】（2017浙江省温州市）小黄准备给长8m，宽6m的长方形客厅铺设瓷砖，现将其划分成一个长方形ABCD区域Ⅰ（阴影部分）和一个环形区域Ⅱ（空白部分），其中区域Ⅰ用甲、乙、丙三种瓷砖铺设，且满足PQ∥AD，如图所示．
（1）若区域Ⅰ的三种瓷砖均价为300元/m2，面积为S（m2），区域Ⅱ的瓷砖均价为200元/m2，且两区域的瓷砖总价为不超过12000元，求S的最大值；
（2）若区域Ⅰ满足BC=2：3，区域Ⅱ四周宽度相等．
①求AB，BC的长；
②若甲、丙两瓷砖单价之和为300元/m2，乙、丙瓷砖单价之比为5：3，且区域Ⅰ的三种瓷砖总价为4800元，求丙瓷砖单价的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
