
【题目】定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a≤b时min{a,b}=a.如:min{1,-3}=﹣3,min{﹣4,﹣2}=﹣4,则min{﹣x2+2,﹣x}的最大值是( )
A. ﹣1 B. ﹣2 C. 1 D. 0
【答案】C
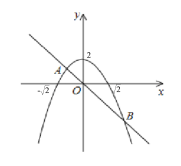
【解析】在同一坐标系xOy中,画出二次函数y=-x2+2与正比例函数y=-x的图象,设它们交于点A、B.结合函数图象进行分析即可.
在同一坐标系xOy中,画出二次函数y=-x2+2与正比例函数y=-x的图象,如图所示.设它们交于点A、B.
令-x2+2=-x,即x2-x-2=0,解得:x1=2,x2=-1,
∴A(-1,1),B(2,-2)
观察图象可知:
①当x≤-1时,min{-x2+2,-x}=-x2+2,函数值随x的增大而增大,其最大值为1;
②当-1<x<2时,min{-x2+2,-x}=-x,函数值随x的增大而减小,没有最大值;
③当x≥2时,min{-x2+2,-x}=-x2+2,函数值随x的增大而减小,最大值为-2.
综上所示,min{-x2+2,-x}的最大值是-1.
故选:C


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】文化是一个国家、一个民族的灵魂,近年来,央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生必须从《经曲咏流传》(记为A)、《中国诗词大会》(记为B)、《中国成语大会》(记为C)、《朗读者》(记为D)中选择自己最喜爱的一个栏目,也可以写出一个自己喜爱的其他文化栏目(记为E).根据调查结果绘制成如图所示的两幅不完整的统计图.
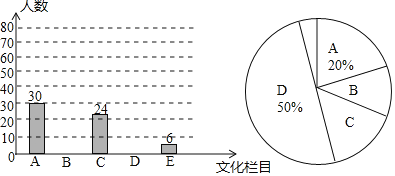
请根据图中信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)将条形统计图补充完整,并求出扇形统计图中“B”所在扇形圆心角的度数;
(3)若选择“E”的学生中有2名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请用列表法或画树状图的方法求出刚好选到同性别学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
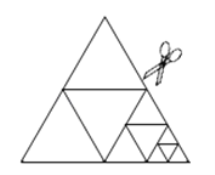
【题目】如图,将一张正三角形纸片剪成四个小正三角形,得到![]() 个小正三角形,称为第一次操作; 然后,将其中的一个正三角形再剪成四个小正三角形,共得到
个小正三角形,称为第一次操作; 然后,将其中的一个正三角形再剪成四个小正三角形,共得到![]() 个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到
个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到![]() 个小正三角形,称为第三次操作;…,根据以上操作,若要得到
个小正三角形,称为第三次操作;…,根据以上操作,若要得到![]() 个小正三角形,则需要操作的次数是__________次.
个小正三角形,则需要操作的次数是__________次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:
①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)构造一个真命题,画图并给出证明;
(2)构造一个假命题,举反例加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
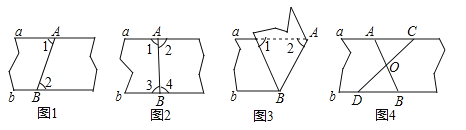
A. 如图1,展开后测得∠1=∠2
B. 如图2,展开后测得∠1=∠2且∠3=∠4
C. 如图3,测得∠1=∠2
D. 如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
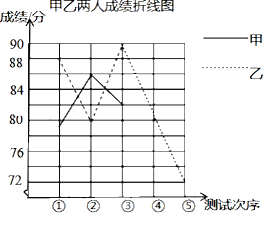
【题目】从甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,对两人进行了五次模拟,并对成绩(单位:分)进行了整理,计算出![]() =83分,
=83分,![]() =82分,绘制成如下尚不完整的统计图表.
=82分,绘制成如下尚不完整的统计图表.
甲、乙两人模拟成绩统计表
① | ② | ③ | ④ | ⑤ | |
甲成绩/分 | 79 | 86 | 82 | a | 83 |
乙成绩/分 | 88 | 79 | 90 | 81 | 72 |
根据以上信息,回答下列问题:
(1)a=
(2)请完成图中表示甲成绩变化情况的折线.
(3)经计算S甲2=6,S乙2=42,综合分析,你认为选拔谁参加比赛更合适,说明理由.
(4)如果分别从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于82分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,一次函数
,一次函数![]() 的图像过点
的图像过点![]() ,且与
,且与![]() 轴及
轴及![]() 的图像分别交于点
的图像分别交于点![]() 、
、![]() ,
,![]() 点坐标为
点坐标为![]() .
.
(1)求n的值及一次函数![]() 的解析式.
的解析式.
(2)求四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),
则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为 ;
(Ⅱ)若点P的“5属派生点”P′的坐标为(3,﹣9),求点P的坐标;
(Ⅲ)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
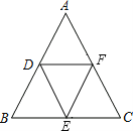
【题目】如图,在△ABC中,∠B=∠C=∠DEF,点D、E、F分别在AB、AC上,且BD=CE.求证:DE=EF.
证明:(请将下面的证明过程补充完整)
∵∠B+∠BDE+∠BED=180°(______)
∠DEF+∠FEC+∠BED=180°(______)
∠B=∠DEF(已知)
∴∠BDE=∠FEC(______)
在△BDE和△CEF中
∠B=∠C(已知)
BD=CE(______)
∠BDE=∠FEC(______)
∴△BDE≌△CEF(______)(用字母表示)
∴DE=EF(______)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com